题目内容
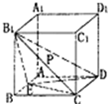 如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E是AB的中点,P是B1C的中点.(Ⅰ)求证:PB∥平面B1ED;
(Ⅱ)求点P到平面B1ED的距离.
考点:点、线、面间的距离计算,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)取B1D的中点O,连接OE,OP,由题设条件推导出OP∥CD,BE∥CD,从而得到PB∥OE,由此能够证明PB∥平面B1ED.
(Ⅱ)由题设条点P到平面B1ED的距离等于点B到平面B1ED的距离,由此利用等积法能求出点P到平面B1ED的距离.
(Ⅱ)由题设条点P到平面B1ED的距离等于点B到平面B1ED的距离,由此利用等积法能求出点P到平面B1ED的距离.
解答:
(Ⅰ)证明:取B1D的中点O,连接OE,OP,
在△B1CD中,P是B1C的中点,O是B1D的中点,
∴OP∥CD,且OP=
CD,
正方形ABCD中,E是AB的中点,
∴BE∥CD,且BE=
CD,
∴OP∥BE且OP=BE,∴PB∥OE,
又PB?平面B1ED,OE?平面B1ED
∴PB∥平面B1ED.…(6分)
(Ⅱ)解:∵PB∥平面B1ED,
∴点P到平面B1ED的距离等于点B到平面B1ED的距离,设其为h,
∵S△BED=
BE•AD=
,
VB1-BED=
S△BED•B1B=
在△B1ED中,B1E=DE=
,B1D=
在△EOD中,可得EO=
=
,
∴S△B1ED=
B1D•EO=
VB-B1ED=
S△B1ED•h=
h,
由VB-B1ED=VB1-BED得,
h=
,∴h=
∴点P到平面B1ED的距离等于
.…(12分)

在△B1CD中,P是B1C的中点,O是B1D的中点,
∴OP∥CD,且OP=
| 1 |
| 2 |
正方形ABCD中,E是AB的中点,
∴BE∥CD,且BE=
| 1 |
| 2 |
∴OP∥BE且OP=BE,∴PB∥OE,
又PB?平面B1ED,OE?平面B1ED
∴PB∥平面B1ED.…(6分)
(Ⅱ)解:∵PB∥平面B1ED,
∴点P到平面B1ED的距离等于点B到平面B1ED的距离,设其为h,
∵S△BED=
| 1 |
| 2 |
| 1 |
| 4 |
VB1-BED=
| 1 |
| 3 |
| 1 |
| 12 |
在△B1ED中,B1E=DE=
| ||
| 2 |
| 3 |
在△EOD中,可得EO=
| DE2-DO2 |
| ||
| 2 |
∴S△B1ED=
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 3 |
| ||
| 12 |
由VB-B1ED=VB1-BED得,
| ||
| 12 |
| 1 |
| 12 |
| ||
| 6 |
∴点P到平面B1ED的距离等于
| ||
| 6 |
点评:本题考查直线与平面平行的证明,考查点到直线的距离的求法,解题时要注意空间思维能力的培养,要注意等积法的合理运用.

练习册系列答案
相关题目
已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,上述命题中真命题的是( )
| A、若a⊥c,b⊥c,则a∥b或a⊥b |
| B、若α⊥β,β⊥γ,则α∥β |
| C、若a?α,b?β,c?β,a⊥b,a⊥c,则α⊥β; |
| D、若a⊥α,b?β,a∥b,则α⊥β |
已知|
|=4,
为单位向量,当
,
的夹角为
时,
+
在
-
上的投影为( )
| a |
| e |
| a |
| e |
| 2π |
| 3 |
| a |
| e |
| a |
| e |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
下列说法不正确的是( )
| A、所有的对立事件都是互斥事件 | ||
B、先后抛掷两枚大小一样的硬币,两枚都出现反面的概率是
| ||
| C、事件“直线y=k(x+1)过点(-1,0)”是必然事件 | ||
D、某红绿灯路口,红灯时间为30秒,黄灯时间为5秒,绿灯时间为45秒,当你到这个路口时,看到黄灯的概率是
|
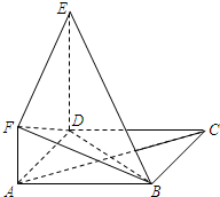 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2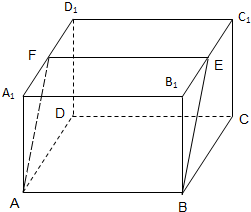 如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2
如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2