题目内容
给出下列四个结论:
①若命题p:?x0R,x02+x0+1<0,则?p:?x∈R,x2+x+1≥0;
②“(x-3)(x-4)=0”是“x-3=0”的充分而不必要条件;
③命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0没有实数根,则m≤0”;
④若a>0,b>0,a+b=4,则
+
的最小值为1.
其中正确结论的个数为( )
①若命题p:?x0R,x02+x0+1<0,则?p:?x∈R,x2+x+1≥0;
②“(x-3)(x-4)=0”是“x-3=0”的充分而不必要条件;
③命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0没有实数根,则m≤0”;
④若a>0,b>0,a+b=4,则
| 1 |
| a |
| 1 |
| b |
其中正确结论的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用命题的否定即可判断出;
②由x-3=0⇒(x-3)(x-4)=0,反之不成立,充分必要条件即可判断出;
③由逆否命题的意义即可得出;
④若a>0,b>0,a+b=4,则
+
=
(a+b)(
+
)化简再利用基本不等式即可得出.
②由x-3=0⇒(x-3)(x-4)=0,反之不成立,充分必要条件即可判断出;
③由逆否命题的意义即可得出;
④若a>0,b>0,a+b=4,则
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| 1 |
| a |
| 1 |
| b |
解答:
解:①利用命题的否定可得:若命题p:?x0R,x02+x0+1<0,则?p:?x∈R,x2+x+1≥0,正确;
②由x-3=0⇒(x-3)(x-4)=0,反之不成立,因此“(x-3)(x-4)=0”是“x-3=0”的必要非充分条件,故不正确;
③由逆否命题的意义可得:命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0没有实数根,则m≤0”,因此正确;
④若a>0,b>0,a+b=4,则
+
=
(a+b)(
+
)=
(2+
+
)≥
(2+2
)=1,当且仅当a=b=2时取等号,因此
+
的最小值为1,因此正确.
综上可知:只有①③④正确.
故选:C.
②由x-3=0⇒(x-3)(x-4)=0,反之不成立,因此“(x-3)(x-4)=0”是“x-3=0”的必要非充分条件,故不正确;
③由逆否命题的意义可得:命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0没有实数根,则m≤0”,因此正确;
④若a>0,b>0,a+b=4,则
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| b |
| a |
| a |
| b |
| 1 |
| 4 |
|
| 1 |
| a |
| 1 |
| b |
综上可知:只有①③④正确.
故选:C.
点评:本题综合考查了简易逻辑的有关知识、基本不等式的性质,属于基础题.

练习册系列答案
相关题目
设a,b,m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(modm).若a=
+
•2+
•22+…+
•220,a≡b(mod10),则b的值可以是( )
| C | 0 20 |
| C | 1 20 |
| C | 2 20 |
| C | 20 20 |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
已知a,b,c是三条不同的直线,α,β,γ是三个不同的平面,上述命题中真命题的是( )
| A、若a⊥c,b⊥c,则a∥b或a⊥b |
| B、若α⊥β,β⊥γ,则α∥β |
| C、若a?α,b?β,c?β,a⊥b,a⊥c,则α⊥β; |
| D、若a⊥α,b?β,a∥b,则α⊥β |
航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( )
| A、12种 | B、16种 |
| C、24种 | D、36种 |
已知|
|=4,
为单位向量,当
,
的夹角为
时,
+
在
-
上的投影为( )
| a |
| e |
| a |
| e |
| 2π |
| 3 |
| a |
| e |
| a |
| e |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
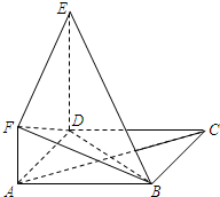 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2