题目内容
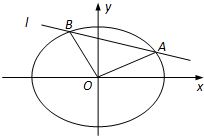 在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为
在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为| 5 |
(1)求椭圆C的方程.
(2)设直线l与椭圆C相交于A,B两点,且∠AOB=
| π |
| 2 |
(3)在(2)的条件下,求AB的最小值.
考点:直线与圆锥曲线的综合问题
专题:
分析:(1)根据题意设椭圆C的方程为
+
=1(a>b>0).再利用已知条件求出a,b的值即可.
(2)设原点O到直线AB的距离为d,则由题设及面积公式知d=
.分情况讨论.当直线OA的斜率不存在或斜率为0时,解得d=
.当直线OA的斜率k存在且不为0时,设直线方程为y=kx.与椭圆方程联立解得A,B两点的坐标,利用d=
.化简即可得到d=
.
(3))d为定值,所以求AB的最小值即求OA•OB的最小值.求AB的最小值即求OA•OB的最小值OA2•OB2=
.利用基本不等式即可求出AB的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
(2)设原点O到直线AB的距离为d,则由题设及面积公式知d=
| |OA|•|OB| |
| |AB| |
2
| ||
| 3 |
| |OA|•|OB| |
| |AB| |
2
| ||
| 3 |
(3))d为定值,所以求AB的最小值即求OA•OB的最小值.求AB的最小值即求OA•OB的最小值OA2•OB2=
k2+
| ||||||
|
解答:
解:(1)由题意,可设椭圆C的方程为
+
=1(a>b>0).
则
,
解得
.
∴椭圆方程为
+
=1.
(2)设原点O到直线AB的距离为d,
则由题设及面积公式知d=
.
①当直线OA的斜率不存在或斜率为0时,
有
或
.
则|AB|=
=3.
∴d=
.
②当直线OA的斜率k存在且不为0时,
则联立方程,得
.
∴
+
=1.
解得
或
在Rt△OAB中,
d2=
=
.
则
=
=
+
=
+
=
+
=
=
+
=
.
∴d=
.
综上,原点O到直线AB的距离为定值
.
(3)∵d为定值,
∴求AB的最小值即求OA•OB的最小值.
OA2•OB2=
=
令t=k2+
,则t≥2,
于是OA2•OB2=
=20•
=20(1-
)
∵t≥2,
∴OA2•OB2≥20(1-
)=
,
当且仅当t=2,即k=±1时,
OA•OB取得最小值
,
∴ABmin=
=
.
∴A的最小值为
.
| x2 |
| a2 |
| y2 |
| b2 |
则
|
解得
|
∴椭圆方程为
| x2 |
| 5 |
| y2 |
| 4 |
(2)设原点O到直线AB的距离为d,
则由题设及面积公式知d=
| |OA|•|OB| |
| |AB| |
①当直线OA的斜率不存在或斜率为0时,
有
|
|
则|AB|=
| 4+5 |
∴d=
2
| ||
| 3 |
②当直线OA的斜率k存在且不为0时,
则联立方程,得
|
∴
| x2 |
| 5 |
| k2x2 |
| 4 |
解得
|
|
在Rt△OAB中,
d2=
| |OA|2•|OB|2 |
| |AB|2 |
| |OA|2•|OB|2 |
| |OA|2+|OB|2 |
则
| 1 |
| d2 |
| |OA|2+|OB|2 |
| |OA|2•|OB|2 |
=
| 1 |
| |OA|2 |
| 1 |
| |OB|2 |
=
| ||||
| 1+k2 |
| ||||
1+
|
=
| ||||
| 1+k2 |
| ||||
| 1+k2 |
=
(
| ||||||||
| 1+k2 |
=
| 1 |
| 4 |
| 1 |
| 5 |
=
| 9 |
| 20 |
∴d=
2
| ||
| 3 |
综上,原点O到直线AB的距离为定值
2
| ||
| 3 |
(3)∵d为定值,
∴求AB的最小值即求OA•OB的最小值.
OA2•OB2=
(1+k2)•(1+
| ||||||||
(
|
=
k2+
| ||||||
|
令t=k2+
| 1 |
| k2 |
于是OA2•OB2=
| t+2 | ||||
|
=20•
| 20t+40 |
| 20t+41 |
=20(1-
| 1 |
| 20t+41 |
∵t≥2,
∴OA2•OB2≥20(1-
| 1 |
| 81 |
| 1600 |
| 81 |
当且仅当t=2,即k=±1时,
OA•OB取得最小值
| 40 |
| 9 |
∴ABmin=
| ||||
|
4
| ||
| 3 |
∴A的最小值为
4
| ||
| 3 |
点评:本题考查椭圆方程的求解,直线与椭圆相结合的问题,利用基本不等式求最值等知识.属于难题.

练习册系列答案
相关题目
已知|
|=4,
为单位向量,当
,
的夹角为
时,
+
在
-
上的投影为( )
| a |
| e |
| a |
| e |
| 2π |
| 3 |
| a |
| e |
| a |
| e |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
下列命题中的假命题是( )
| A、?x∈R,2x-1>0 |
| B、?x∈R,lgx<1 |
| C、?x∈N+,(x-1)2>0 |
| D、?x∈R,tanx=2 |
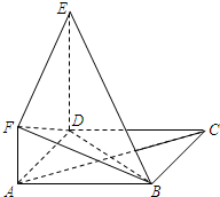 如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2
如图,正方形ABCD与直角梯形ADEF所在平面互相垂直,∠ADE=90°,AF∥DE,DE=DA=2AF=2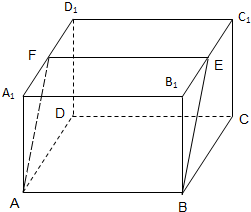 如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2
如图,直四棱柱ABCD-A1B1C1D1的底面边长为2的菱形,∠BAD=60°,高为1,过底边AB作一截面ABEF,若BE=2