题目内容
20. 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点,设AC中点为O.(1)求证:平面EFO∥平面PAD
(2)若∠PDA=45°,求EF与平面ABCD所成的角的大小.
分析 (1)连AC,设AC中点为O,连OF、OE,证明FO∥PA,EO∥BC,利用BC∥AD∴EO∥AD证明平面EFO∥平面PAD.(2)说明∠FEO为EF与平面ABCD所成的角的大小.利用△FOE是直角三角形推出结果.
解答 (12分)证明:连AC,设AC中点为O,连OF、OE
(1)在△PAC中,∵F、O分别为PC、AC的中点
∴FO∥PA …①在△ABC中,
∵E、O分别为AB、AC的中点∴EO∥BC,又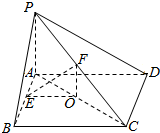
∵BC∥AD∴EO∥AD …②
综合①、②可知:平面EFO∥平面PAD …..6′
(2)若∠PDA=45°?,则 PA=AD=BC,
∵EO$\stackrel{∥}{=}\frac{1}{2}BC$,FO$\stackrel{∥}{=}\frac{1}{2}PA$,
∴FO=EO 又∵FO⊥平面AC
∴∠FEO为EF与平面ABCD所成的角的大小.
∴△FOE是直角三角形,
∴?FEO=45°?…..12′.
点评 本题考查平面与平面平行的判定定理的应用,直线与平面所成角的求法,考查计算能力.

练习册系列答案
相关题目
11.(1)某社区有500户家庭,其中高收入家庭125户,中等收入家庭280户,低收入家庭95户,为了了解社会购买力的某种指标,要从中抽取一个容量为100户的样本;
(2)从10名同学中抽取3人参加座谈会.
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 ( )
(2)从10名同学中抽取3人参加座谈会.
a简单随机抽样 b系统抽样 c分层抽样
问题与方法配对正确的是 ( )
| A. | (1)a,(2)c | B. | (1)a,(2)b | C. | (1)c,(2)a | D. | (1)c,(2)b |
12.在正方体ABCD-A1B1C1D1中,点P为正方形A1B1C1D1内部及边上的动点,且BD⊥平面AA1P,则直线BP与AD1所成角θ的取值范围是( )
| A. | 0<θ≤$\frac{π}{3}$ | B. | 0<θ≤$\frac{π}{2}$ | C. | 0≤θ≤$\frac{π}{3}$ | D. | 0≤θ≤$\frac{π}{2}$ |
 如图,设计一副矩形宣传画,要求画面面积为96cm2,画面上下边还要留3cm空白,左右要留2cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画面所用纸张面积最小?
如图,设计一副矩形宣传画,要求画面面积为96cm2,画面上下边还要留3cm空白,左右要留2cm空白,怎样确定画面的高与宽的尺寸,才能使宣传画面所用纸张面积最小?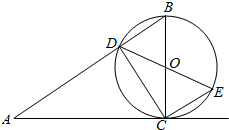 如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.
如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.