题目内容
已知向量
=（cos3x，sin3x），
=（cosx，-sinx），且x∈[0，
]，求f（x）=λ
•
-λ|
+
|•sin2x（λ≠0）的单调区间．
| a |
| b |
| π |
| 4 |
| a |
| b |
| a |
| b |
考点：三角函数中的恒等变换应用
专题：三角函数的求值,三角函数的图像与性质,平面向量及应用
分析：利用三角函数中的恒等变换应用，可得f（x）=λ
•
-λ|
+
|•sin2x=
λcos（4x+
），利用余弦函数的单调性即可求得f（x）=λ
•
-λ|
+
|•sin2x（λ≠0）的单调区间．
| a |
| b |
| a |
| b |
| 2 |
| π |
| 4 |
| a |
| b |
| a |
| b |
解答：
解：∵x∈[0，
]，
∴2x∈[0，
]，
∴|cos2x|=cos2x，
∴f（x）=λ
•
-λ|
+
|•sin2x
=λ（cos3xcosx-sin3xsinx）-λ|（cos3x+cosx），（sin3x-sinx）|•sin2x
=λcos4x-λsin2x•
=λcos4x-λsin2x•
=λcos4x-λsin2x•2|cos2x|
=λcos4x-λsin2x•2cos2x
=λ（cos4x-sin4x）
=
λcos（4x+
）．
由2kπ-π≤4x+
≤2kπ（k∈Z）得：
-
≤x≤
-
（k∈Z）；
由2kπ≤4x+
≤2kπ+π（k∈Z）得：
-
≤x≤
+
（k∈Z）；
当λ＞0时，f（x）的递增区间为[
-
，
-
]，递减区间为[
-
，
+
]（k∈Z）；
当λ＜0时，f（x）的递减区间为[
-
，
-
]，递增区间为[
-
，
+
]（k∈Z）．
| π |
| 4 |
∴2x∈[0，
| π |
| 2 |
∴|cos2x|=cos2x，
∴f（x）=λ
| a |
| b |
| a |
| b |
=λ（cos3xcosx-sin3xsinx）-λ|（cos3x+cosx），（sin3x-sinx）|•sin2x
=λcos4x-λsin2x•
| (cos3x+cosx)2+(sin3x-sinx)2 |
=λcos4x-λsin2x•
| 2+2cos4x |
=λcos4x-λsin2x•2|cos2x|
=λcos4x-λsin2x•2cos2x
=λ（cos4x-sin4x）
=
| 2 |
| π |
| 4 |
由2kπ-π≤4x+
| π |
| 4 |
| kπ |
| 2 |
| 5π |
| 16 |
| kπ |
| 2 |
| π |
| 16 |
由2kπ≤4x+
| π |
| 4 |
| kπ |
| 2 |
| π |
| 16 |
| kπ |
| 2 |
| 3π |
| 16 |
当λ＞0时，f（x）的递增区间为[
| kπ |
| 2 |
| 5π |
| 16 |
| kπ |
| 2 |
| π |
| 16 |
| kπ |
| 2 |
| π |
| 16 |
| kπ |
| 2 |
| 3π |
| 16 |
当λ＜0时，f（x）的递减区间为[
| kπ |
| 2 |
| 5π |
| 16 |
| kπ |
| 2 |
| π |
| 16 |
| kπ |
| 2 |
| π |
| 16 |
| kπ |
| 2 |
| 3π |
| 16 |
点评：本题考查三角函数中的恒等变换应用，着重考查向量的坐标运算及二倍角的正弦、余弦公式的应用，考查余弦函数的单调性质，考查综合运算、求解能力，属于难题．
练习册系列答案
相关题目
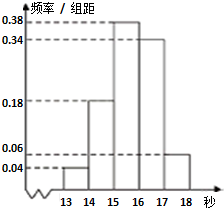南山中学高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．