题目内容
设函数f（x）=x3-3x2+3x-1，记a=f（-
），b=f（
），c=f（
），则（ ）
| 5 |
| 3 |
| 7 |
| A、b＜a＜c |
| B、c＜b＜a |
| C、a＜c＜b |
| D、a＜b＜c |
考点：函数的值
专题：函数的性质及应用
分析：利用导数的性质求解．
解答：
解：∵函数f（x）=x3-3x2+3x-1，
∴f′（x）=3x2-6x+3=3（x2-2x+1）=3（x-1）2≥0，
∴f（x）在R上是增函数，
∵
＞
＞-
，
∴a＜b＜c．
故选：D．
∴f′（x）=3x2-6x+3=3（x2-2x+1）=3（x-1）2≥0，
∴f（x）在R上是增函数，
∵
| 7 |
| 3 |
| 5 |
∴a＜b＜c．
故选：D．
点评：本题考查三个数的大小的比较，是基础题，解题时要认真审题，注意函数值的合理运用．
练习册系列答案
相关题目
若函数f（x）=x3-3x在（a，6-a2）上有最小值，则实数a的取值范围是（ ）
A、（-
| ||
B、[-
| ||
| C、[-2，1） | ||
| D、（-2，1） |
若f（x）=3sin（ωx+φ）（ω＞0，|φ|＜
）的周期为π且图象关于x=
对称，则（ ）
| π |
| 2 |
| 2π |
| 3 |
A、f（x）的图象过点（0，
| ||||
B、f（x）在[
| ||||
| C、将f（x）的图象向右平移|φ|个单位得到函数y=3sinωx的图象 | ||||
D、f（x）的一个对称中心是（
|
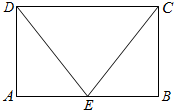如图，矩形ABCD中，点E为边AB的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△AED或△BEC内部的概率等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
tan12°-
| ||
| sin6°sin84° |
| A、4 | B、8 | C、16 | D、32 |
设函数y=sinx的定义域为[a，b]，值域为[-
，1]，给出以下四个结论：
①b-a的最小值为
②b-a的最大值为
③a可能等于2kπ-
（k∈z）
④b可能等于2kπ-
（k∈z）
其中正确的有（ ）
| 1 |
| 2 |
①b-a的最小值为
| 2π |
| 3 |
②b-a的最大值为
| 4π |
| 3 |
③a可能等于2kπ-
| π |
| 6 |
④b可能等于2kπ-
| π |
| 6 |
其中正确的有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
A={x|y=
}，B={y|y=
}，则A∪B=（ ）
| 2x-x2 |
| x2+1 |
| x2 |
| A、（1，2] |
| B、[0，1）∪（1，2] |
| C、[0，+∞] |
| D、[0，2] |
下列图形中，哪个是函数y=|-x2+2x|的简图（ ）
A、 |
B、 |
C、 |
D、 |