题目内容
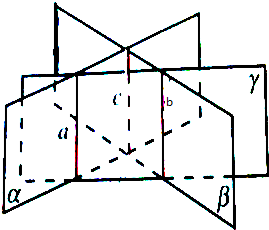
如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为2m，则这个六棱柱的体积为考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：由题意，设正六棱柱的底面边长为am；高为hm；从而可得2ah=4，
a=2，从而求体积．
| 3 |
解答：
解：由题意，设正六棱柱的底面边长为am；高为hm；
则2ah=4，
a=2，
解得，a=
，h=
，
故V=Sh=6×
×（
）2×sin60°×
=6；
故答案为：6m3．
则2ah=4，
| 3 |
解得，a=
2
| ||
| 3 |
| 3 |
故V=Sh=6×
| 1 |
| 2 |
2
| ||
| 3 |
| 3 |
故答案为：6m3．
点评：本题考查了空间几何体的体积的求法，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
若m＞0，n＞0，a＞0且a≠1，则下列等式中正确的是（ ）
| A、（am）n=am+n | |||||
B、a
| |||||
| C、logam÷logan=loga（m-n） | |||||
D、
|
已知复数z1=2+ai（a∈R），z2=1-2i，若
为纯虚数，则|z1|=（ ）
| z1 |
| z2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知sin（π+α）=
，且α是第四象限角，则cos（α-2π）的值是（ ）
| 2 |
| 3 |
A、±
| ||||
B、
| ||||
C、±
| ||||
D、
|
