题目内容
下面是一个2×2的列联表
|
| y1 | y2 | 总计 |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 合计 | 54 | b | 100 |
则表中a、b的值依次为( )
A.44,54 B.52,46
C.54,46 D.52,54
B

某学校为了了解学生的日平均睡眠时间(单位:h),随机选择了n名同学进行调查.下表是这n名同学的日睡眠时间的频率分布表.
| 序号(i) | 分组(睡眠时间) | 频数(人数) | 频率 |
| 1 | [4,5) | 6 | 0.12 |
| 2 | [5,6) |
| 0.20 |
| 3 | [6,7) | a | |
| 4 | [7,8) | b | |
| 5 | [8,9) |
| 0.08 |
(1)求n的值.若a=20,将表中数据补全,并画出频率分布直方图.
(2)统计方法中,同一组数据常用该组区间的中点值(例如区间[4,5)的中点值是4.5)作为代表.若据此计算的上述数据的平均值为6.52,求a、b的值,并由此估计该学校学生的日平均睡眠时间在7小时以上的概率.
甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为t(cm),相关行业质检部门规定:若t∈(2.9,3.1],则该零件为优等品;若t∈(2.8,2.9]∪(3.1,3.2],则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
| 尺寸 | [2.7, 2.8] | (2.8, 2.9] | (2.9, 3.0] | (3.0, 3.1] | (3.1, 3.2] | (3.2, 3.3] |
| 甲机床零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
| 乙机床零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(1)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(2)对于这两台机床生产的零件,在排除其他因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式:K2=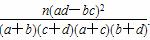 .
.
参考数据:
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |

 x+1上,则这组样本数据的样本相关系数为( )
x+1上,则这组样本数据的样本相关系数为( )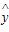 =
=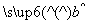 x+
x+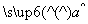 ,则“(x0,y0)满足线性回归方程
,则“(x0,y0)满足线性回归方程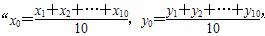 的( )
的( ) 和
和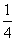 ,则该市足球队夺得全省足球冠军的概率是________.
,则该市足球队夺得全省足球冠军的概率是________.