题目内容
设A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的两点,并且满足OA⊥OB,则y1y2等于( )
A.-4p2 B.-3p2
C.-2p2 D.-p2
A
[解析] ∵OA⊥OB,∴ =0.①
=0.①
∴x1x2+y1y2=0.
∵A、B都在抛物线上,
代入①得 ·
· +y1y2=0,解得y1y2=-4p2.
+y1y2=0,解得y1y2=-4p2.

练习册系列答案
相关题目
下面是一个2×2的列联表
|
| y1 | y2 | 总计 |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 合计 | 54 | b | 100 |
则表中a、b的值依次为( )
A.44,54 B.52,46
C.54,46 D.52,54
 +
+ =1上,若A点坐标为(3,0),|
=1上,若A点坐标为(3,0),| |=1,且
|=1,且 ·
· 等于( )
等于( )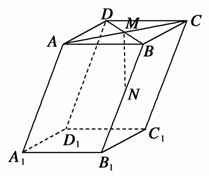
 a+
a+ c
c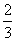 c
c ·
· 是一个定值.
是一个定值. B.
B.
 D.
D.