题目内容
20.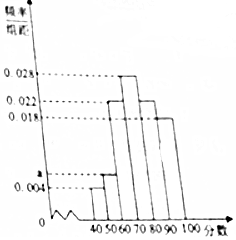 高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].(1)求频率分布图中a的值;
(2)求该班50名学生中,成绩不低于80分的概率;
(3)从成绩在[40,60)的学生中,随机抽取2人,求此2人分数都在[40,50)的概率.
分析 (1)由频率分布直方图中小矩形面积之和为1,能求出a.
(2)由所给频率分布直方图知,50名学生成绩不低于80的频率为0.4,由此能求出该班成绩不低于80的概率的估计值.
(3)学生成绩在[50,60)的有3人,记为A1,A2,A3,学生成绩在[40,50)的有2人,记为B1,B2.由此能求出此2人分数都在[40,50)的概率.
解答 解:(1)因为(0.004+a+0.018+0.022+0.028)×10=1,
所以a=0.006.…(3分)
(2)由所给频率分布直方图知,50名学生成绩不低于80的频率为(0.022+0.018)×10=0.4,
所以该班成绩不低于80的概率的估计值为0.4.…(7分)
(3)学生成绩在[50,60)的有:50×0.006×10=3(人),记为A1,A2,A3,
学生成绩在[40,50)的有:50×0.004×10=2(人),记为B1,B2.
从这5名学生中随机抽取2人,所有可能的结果共有10种,
它们是{A1,A2},{A1,A3},{A1,B1},{A1,B2},{A2,B3},{A2,B1},{A2,B2},{A3,B1},{A3,B2},{B1,B2},
又因为所抽取2人的成绩都在[40,50)的结果有1种,即{B1,B2},
故所求的概率为p=$\frac{1}{10}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真是题,注意列举法的合理运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.已知向量$\overrightarrow a=(1,2)$,$\overrightarrow b=(1,0)$,$\overrightarrow c=(3,4)$,若λ为实数,$(\overrightarrow a+λ\overrightarrow b)⊥\overrightarrow c$,则λ=( )
| A. | $\frac{5}{3}$ | B. | $\frac{1}{2}$ | C. | $-\frac{5}{2}$ | D. | $-\frac{11}{3}$ |
8.已知$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(1,6),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
5.已知集合M={0,2},则M的真子集的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.已知两条直线y=ax-2和3x-(a+2)y+1=0互相平行,则a等于( )
| A. | -1或3 | B. | -1或3 | C. | 1或3 | D. | 1或-3 |
10.△ABC各角的对应边分别为a,b,c,满足$\frac{a}{b+c}+\frac{b}{a+c}≥1$,则角C的范围是( )
| A. | $(0,\frac{π}{3}]$ | B. | $(0,\frac{π}{6}]$ | C. | $[\frac{π}{3},π)$ | D. | $[\frac{π}{6},π)$ |