题目内容
10.若x是方程${2^x}-\frac{3}{{{2^{x-1}}}}=5$的解,化简:|x-3|+x.分析 设2x=t,t>0,原方程转化为t2-5t-6=0,从而求出x=log26,由此能化简|x-3|+x.
解答 解:设2x=t,t>0,
∵${2^x}-\frac{3}{{{2^{x-1}}}}=5$,
∴t2-5t-6=0,
解得t=6或t=-1(舍),
∴2x=6,则x=log26,
∴|x-3|+x=|log26-3|+log26=3-log26+log26=3.
点评 本题考查代数式的化简,是基础题,解题时要认真审题,注意指数方程的性质的合理运用.

练习册系列答案
相关题目
18.直线2x-y-4=0与抛物线y2=6x交于A、B两点,则线段AB的长度为( )
| A. | $\frac{{\sqrt{265}}}{2}$ | B. | $\frac{{\sqrt{285}}}{2}$ | C. | $\frac{{\sqrt{305}}}{2}$ | D. | $\frac{{\sqrt{335}}}{2}$ |
2.下列函数中,既是偶函数,又是在区间(0,+∞)上单调递减的是( )
| A. | $y=\frac{1}{x}$ | B. | y=2|x| | C. | $y=ln\frac{1}{|x|}$ | D. | y=x3 |
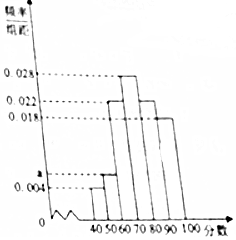 高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
高三(3)班班主任根据本班50名学生体能测试成绩,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].