题目内容
17.已知抛物线C:x2=2y的焦点为F,过抛物线上一点M作抛物线C的切线l,l交y轴于点N.(1)判断△MFN的形状;
(2)若A,B两点在抛物线C上,点D(1,1)满足$\overrightarrow{AD}$+$\overrightarrow{BD}$=$\overrightarrow{0}$,若抛物线C上存在异于A,B的点E,使得经过A,B,E三点的圆与抛物线在点E处的有相同的切线,求点E的坐标.
分析 (1)利用导数求得切线方程,当x=0,求得N点坐标,根据抛物线的焦半径公式,即可求得丨MF丨=丨NF丨,则△MFN为等腰三角形;
(2)根据向量的坐标运算,求得B点坐标,分别求得AE及AB的中垂线方程,即可求得△ABE外接圆的圆心,由kME•x0=-1,即可求得点E的坐标.
解答 解:(1)由题意可知:抛物线C:x2=2y的焦点F(0,$\frac{1}{2}$),
设M(x1,$\frac{{x}_{1}^{2}}{2}$),由y=$\frac{{x}^{2}}{2}$,y′=x,
则切线l的方程y-$\frac{{x}_{1}^{2}}{2}$=x1(x-x1),则y=x1x-$\frac{{x}_{1}^{2}}{2}$,
∴N(0,$\frac{{x}_{1}^{2}}{2}$),丨MF丨=$\frac{{x}_{1}^{2}}{2}$+$\frac{1}{2}$,丨NF丨=$\frac{{x}_{1}^{2}}{2}$+$\frac{1}{2}$,
丨MF丨=丨NF丨,
∴△MFN为等腰三角形;
(2)设A(x2,$\frac{{x}_{2}^{2}}{2}$),由$\overrightarrow{AD}$+$\overrightarrow{BD}$=$\overrightarrow{0}$,
∴D(1,1)是AB的中点,B(2-x2,2-$\frac{{x}_{2}^{2}}{2}$),
由B在抛物线C上,则(2-x2)2=2(2-$\frac{{x}_{2}^{2}}{2}$),
解得:x2=0,x2=2,
∴A,B两点的坐标为(0,0),(2,2),
设E(x0,$\frac{{x}_{0}^{2}}{2}$),(x0≠0,x0≠2),
AB的中垂线方程y=-x+2,①AE的中垂线方程y=-$\frac{2}{{x}_{0}}$x+1+$\frac{{x}_{0}^{2}}{4}$,②
由
由①②解得:圆心M(-$\frac{{x}_{0}^{2}+2{x}_{0}}{4}$,$\frac{{x}_{0}^{2}+2{x}_{0}+8}{4}$),
由kME•x0=-1,整理得:x02-x0-2=0,
解得:x0=-1或x0=2,由x0≠0,x0≠2,
∴x0=-1,
∴E点坐标为(-1,$\frac{1}{2}$).
点评 本题考查直线与抛物线的位置关系,向量数量积的坐标运算,三角形外接圆的求法,考查计算能力,属于中档题.

(1)求数列{an}的通项公式;
(2)若数列{an}的前n项和为Sn,且Sn=21,求n的值.
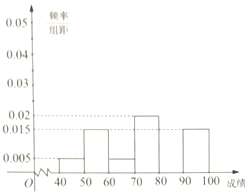
(1)班20名同学成绩频率分布直方图
(2)班20名同学成绩茎叶图
| 4 | 5 |
| 5 | 2 |
| 6 | 4 5 6 8 |
| 7 | 0 5 5 8 8 8 8 9 |
| 8 | 005 5 |
| 9 | 45 |
(Ⅱ)从(2)班参加测试的不低于80分的同学中随机选取两人,求这两人中至少有1人的成绩在90分以上的概率;
(III )运用所学统计知识分析比较两个班学生的古诗词水平.