题目内容
f(x)是定义在R上的偶函数,且在(0,+∞)上是减函数,若x2>x1,x1+x2>0,则下列说法正确的是( )
| A、f(x1)>f(x2) |
| B、f(x1)=f(x2) |
| C、f(x1)<f(x2) |
| D、f(x1)和f(x2)的大小关系不能确定 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据题意得出|x2|>|x1|,运用(0,+∞)上是减函数,得出f(|x2|)<f(|x1|),再运用f(x)=f(-x)=f(|x|),求解即可.
解答:
解:∵x2>x1,x1+x2>0,
∴x2>-x1,|x2|>|x1|
∵f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=f(|x|),
∵在(0,+∞)上是减函数,
∴f(|x2|)<f(|x1|),
即f(x2)<f(x1),
故选:A
∴x2>-x1,|x2|>|x1|
∵f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=f(|x|),
∵在(0,+∞)上是减函数,
∴f(|x2|)<f(|x1|),
即f(x2)<f(x1),
故选:A
点评:本题考查了偶函数的单调性,关键转化到给定的区间求解,属于中档题,本题是常规考查的题目,熟练运用f(x)=f(-x)=f(|x|).

练习册系列答案
相关题目
设f(n)>0(n∈N*),f(2)=4,并且对于任意n2,n2∈N*,有f(n1+n2)=f(n1)•f(n2)成立,猜想f(n)的表达式为( )
| A、f(n)=n2 |
| B、f(n)=2n |
| C、f(n)=2n+1 |
| D、f(n)=2n |

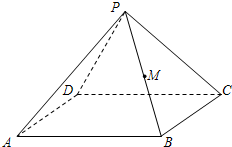 四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点
四棱锥P-ABCD中,棱长PD=a,底面ABCD是边长为a的菱形,点M为PB中点