题目内容
7.已知商场销售某种茶杯购买人数n与茶杯标价x元满足关系式:n=-x+b(b为常数).把购买人数为零时的最低标价称为无效价格,已知无效价格为每个30元.现在这种茶杯的成本价是10/个,商场以高于成本价的相同价格(标价)出售. 问:(1)求b的值;
(2)商场要获取最大利润,茶杯的标价应定为每件多少元?
(3)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么茶杯的标价为每个多少元?
分析 (1)由n=-x+b及无效价格为30/个,求出b;
(2)求出利润函数,由二次函数求最值;
(2)由题意得,(x-10)(-x+30)=100×75%,即可得出结论.
解答 解:(1)由n=-x+b及无效价格为30/个,得0=-30+b,∴b=30. (2分)
(2)由(1),得n=-x+30.设茶杯利润为y元,则 (3分)
y=(x-10)(-x+30)=-x2+40x-300=-(x-20)2+100,x∈(10,30]. (5分)
当x=20时,ymax=100. (6分)
故商场要获取最大利润,茶杯的标价应定为每个20元. (7分)
(3)由题意得,(x-10)(-x+30)=100×75%,即x2-40x+375=0. (10分)
解得x1=15,x2=25. (11分)
故商场要获取最大利润的75%,根据客观实际,每个标价应为15元. (12分)
点评 本题考查了学生将实际问题转化为数学问题的能力及函数的性质应用,属于中档题.

练习册系列答案
相关题目
17.为了得到函数y=sin(2x-$\frac{π}{3}$)的图象,只需将函数y=sin2x的图象上所有的点( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向左平移$\frac{π}{3}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
18.已知三棱锥P-ABC的四个顶点P,A,B,C都在半径为R的同一个球面上,若PA,PB,PC两两相互垂直,且PA=1,PB=2,PC=3,则R等于( )
| A. | $\frac{{\sqrt{14}}}{2}$ | B. | $\sqrt{14}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\sqrt{3}$ |
15.已知向量$\overrightarrow a=({m,1}),\overrightarrow b=({1,n-2}),({m>0,n>0})$若$\overrightarrow a⊥\overrightarrow b$,则$\frac{1}{m}+\frac{2}{n}$的最小值为( )
| A. | 2$\sqrt{2}$ | B. | $\frac{3}{2}$+$\sqrt{2}$ | C. | 3$\sqrt{2}$+2 | D. | 2$\sqrt{2}$+3 |
2.设函数$f(x)=\left\{\begin{array}{l}3x+1,x<1\\{2^{x+b}},x≥1\end{array}\right.$,若$f[f(\frac{2}{3})]=4$,则b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
16.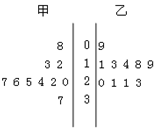 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )| A. | 甲的极差是29 | B. | 甲的中位数是25 | ||
| C. | 乙的众数是21 | D. | 甲的平均数比乙的大 |
17.下列命题中正确的是( )
| A. | 若p:?x∈R,ex>xe,q:?x0∈R,|x0|≤0,则(¬p)∧q为假 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |