题目内容

已知函数f（x）=
3
Asinxcosx+Acos2x-
A
2
（x∈RA为常数且A＞0）的最大值为2．
（1）求f（π）的值；
（2）若sinθ=-
3
5
，θ∈（-
π
2
，0），求f（θ+
π
6
）．
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：利用二倍角公式将函数化简，根据最大值求出A，对于（1），直接代入运算即可
对于（2），同样代入运算．
解答： 解：f（x）=
3
Asinxcosx+Acos2x-
A
2
=Asin（2x+
π
6
），
∵A＞0，函数最大值为2，∴A=2，∴f（x）=2sin（2x+
π
6
）
（1）∴f（π）=2sin（π+
π
6
）=1
（2）f（θ+
π
6
）=2sin[2（θ+
π
6
）+
π
6
]=2cos2θ=2（1-2sin2θ）=
14
25
点评：本题考查三角函数的恒等变换，属于基础题．
练习册系列答案
相关题目
如图所示的是一个算法的流程图，当输入x的值为2014时，输出y的值为 （　　）
A、1
B、
1
3
C、
1
9
D、9
若某几何体的三视图（单位：cm）如图所示，则此几何体的体积为（　　）
A、30B、24C、10D、6
已知tan（
π
6
+α）=3，α为锐角，则cos（
π
3
-α）=（　　）
A、
3
10
10
B、-
3
10
10
C、
10
10
D、-
10
10
执行如图所示的程序框图，输出的结果是15，则a的初始值m（m＞0）有多少种可能（　　）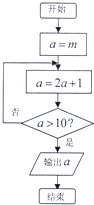
A、1B、2C、3D、4
已知A，B，C为△ABC的三个内角，向量
α
=（cos
A-B
2
，
3
sin
A+B
2
），|
α
|=
2
．如果当C最大时，存在动点M，使得|
MA
|，|
AB
|，|
MB
|成等差数列，则
|
MC
|
|
AB
|
最大值是
 
．
某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为A配方和B配方）做试验，各生产了100件这种产品，并测试了每件产品的质量指标值，得到下面试验结果：
A配方的频率分布表
指标值分组 〔90，94） 〔94，98） 〔98，102） 〔102，106） 〔106，110〕
频数 8 20 42 22 8
B配方的频率分布表
指标值分组 〔90，94） 〔94，98） 〔98，102） 〔102，106） 〔106，110〕
频数 4 12 42 32 10
（Ⅰ）分别估计用A配方，B配方生产的产品的优质品率；
（Ⅱ）已知用B配方生成的一件产品的利润y（单位：元）与其质量指标值t的关系式为yy=
-2， t＜94
2 ，94≤t＜102
4，t≥102

从用B配方生产的产品中任取一件，其利润记为X（单位：元），求X的分布列及数学期望．（以实验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）
已知数列{an}的前n项和为sn，a1=1，当n∈N+有an+1=
Sn
n
+n+1．
（1）求{an}的通项公式
（2）记bn=
1
an
，求证：b1+b2+…+bn≤
2n-1
．
已知函数f（x）=
1
3
x3-
1
2
（a+2）x2+2ax-a2（a∈R）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若a=4，y=f（x）的图象与直线y=m有三个交点，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网