题目内容
17.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{{2}^{-|x-1|}+1,(x≠1)}\\{a,(x=1)}\end{array}\right.$,若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是( )| A. | (0,1) | B. | $(0,\frac{3}{2})$ | C. | (1,2) | D. | $(1,\frac{3}{2})∪$$(\frac{3}{2},2)$ |
分析 作出f(x)的图象,利用换元法结合一元二次函数的图象和性质即可.
解答 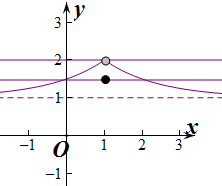 解:作出f(x)的图象如图:设t=f(x),
解:作出f(x)的图象如图:设t=f(x),
则方程等价为2t2-(2a+3)t+3a=0,
由图象可知,
若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,
∴即要求对应于f(x)等于某个常数有3个不同实数解,
∴故先根据题意作出f(x)的简图:
由图可知,只有当f(x)=a时,它有三个根.
所以有:1<a<2 ①.
再根据2f2(x)-(2a+3)f(x)+3a=0有两个不等实根,
则判别式△=(2a+3)2-4×2×3a>0,
解得a≠$\frac{3}{2}$,
故1<a<$\frac{3}{2}$或$\frac{3}{2}$<x<2,
故选:D.
点评 本题主要考查函数和方程的应用,利用换元法结合一元二次函数的图象和性质,利用数形结合是解决本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
6.sin20°cos170°-cos20°sin10°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
7.设集合A={x|-5<x<3},集合B=N,则A∩B=( )
| A. | {1,2} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |