题目内容
18.在△ABC中,角A,B,C所对的边分别是a,b,c,设向量$\overrightarrow m$=(2cosC,$\frac{c}{2}$-b),$\overrightarrow{n}$=($\frac{a}{2}$,1),且$\overrightarrow m⊥\overrightarrow n$.(Ⅰ)求角A的值;
(Ⅱ)若a=2,求△ABC的周长l的取值范围.
分析 (Ⅰ)根据向量垂直以及正弦定理求出A的值即可;(Ⅱ)根据正弦定理求出b,c,表示出三角形的周长l,结合三角函数的性质求出l的范围即可.
解答 解:(Ⅰ)$\overrightarrow m⊥\overrightarrow n⇒\overrightarrow m•\overrightarrow n=0$,$\frac{a}{2}•2cosC+\frac{c}{2}-b=0$,
在△ABC中,由正弦定理得:$sinAcosC+\frac{1}{2}sinC-sinB=0$,
sinB=sin[π-(A+C)]=sin(A+C)=sinAcosC+cosAsinC代入上式得:
$cosAsinC=\frac{1}{2}sinC∴cosA=\frac{1}{2}$,∴$A=\frac{π}{3}$,
(Ⅱ)由正弦定理:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}$
得:$b=\frac{4}{{\sqrt{3}}}sinB,c=\frac{4}{{\sqrt{3}}}sinC=\frac{4}{{\sqrt{3}}}sin[π-(A+B)]=\frac{4}{{\sqrt{3}}}sin(B+\frac{π}{3})$,
∴$l=a+b+c=2+\frac{4}{{\sqrt{3}}}sinB+\frac{4}{{\sqrt{3}}}sin(B+\frac{π}{3})$,
$\begin{array}{l}=2+\frac{4}{{\sqrt{3}}}(sinB+\frac{1}{2}sinB+\frac{{\sqrt{3}}}{2}cosB)=2+4(\frac{{\sqrt{3}}}{2}sinB+\frac{1}{2}cosB)\\=2+4sin(B+\frac{π}{6})\end{array}$,
∵$0<B<\frac{2π}{3}$∴$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,
∴$\frac{1}{2}<sin(B+\frac{π}{6})≤1$,
∴l∈(4,6].
点评 本题考查了正弦定理的应用,考查三角函数的性质以及向量的垂直的性质,是一道中档题.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案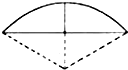 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )| A. | 6平方米 | B. | 9平方米 | C. | 12平方米 | D. | 15平方米 |
| A. | (0,1) | B. | $(0,\frac{3}{2})$ | C. | (1,2) | D. | $(1,\frac{3}{2})∪$$(\frac{3}{2},2)$ |
 满足约束条件
满足约束条件 ,那么
,那么 的最大值是__________.
的最大值是__________. ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.