题目内容
19.袋中有10个大小形状完全相同的小球,其中6个红球,4个白球,每次从中任意摸出一个小球,连续摸三次.(1)若采取不放回抽样方式,求摸出的三球中至少有两个红球的概率;
(2)若采取有放回抽样方式,求摸出的三球中红球少于两个的概率.
分析 使用组合数公式分别求出基本事件总个数和符合条件的基本事件个数,使用古典概型的概率计算公式求出概率.
解答 解:(1)若采取不放回抽样方式,从10个小球中取出3个,共有C${\;}_{10}^{3}$=120个基本事件,
其中有2个红球的基本事件有${C}_{6}^{2}$C${C}_{4}^{1}$=60个,有3个红球的基本事件有${C}_{6}^{3}$C${\;}_{4}^{0}$=20个.
∴摸出的三球中至少有两个红球的概率P=$\frac{60+20}{120}=\frac{2}{3}$.
(2)若采取有放回抽样方式,则抽取三次共有${C}_{10}^{1}{C}_{10}^{1}{C}_{10}^{1}$=1000个基本事件,
则摸出的小球中没有红球的基本事件有C${\;}_{4}^{1}$C${\;}_{4}^{1}$${C}_{4}^{1}$=64个,
摸出的小球中有一个红球的基本事件有3${C}_{6}^{1}$C${\;}_{4}^{1}$${C}_{4}^{1}$=288个,
∴摸出的三球中红球少于两个的概率P=$\frac{64+288}{1000}$=$\frac{44}{125}$.
点评 本题考查了古典概型的概率计算公式,属于基础题.

练习册系列答案
相关题目
10.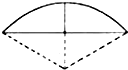 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
 《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为$\frac{2π}{3}$,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )| A. | 6平方米 | B. | 9平方米 | C. | 12平方米 | D. | 15平方米 |
17.设定义域为R的函数f(x)=$\left\{\begin{array}{l}{{2}^{-|x-1|}+1,(x≠1)}\\{a,(x=1)}\end{array}\right.$,若关于x的方程2f2(x)-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是( )
| A. | (0,1) | B. | $(0,\frac{3}{2})$ | C. | (1,2) | D. | $(1,\frac{3}{2})∪$$(\frac{3}{2},2)$ |