题目内容
3.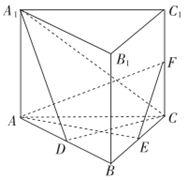 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.(1)证明:平面AEF⊥平面B1BCC1;
(2)若D为AB中点,∠CA1D=30°且AB=4,求三棱锥F-AEC的体积.
分析 (1)由三棱柱ABC-A1B1C1是直三棱柱,可得AE⊥BB1,又E是正三角形ABC的边BC的中点,求出AE⊥BC,又BC∩BB1=B,则AE⊥平面B1BCC1,而AE?平面AEF,即可证得平面AEF⊥平面B1BCC1;
(2)由△ABC是正三角形,可得CD⊥AB,又三棱柱ABC-A1B1C1是直三棱柱,可得CD⊥AA1,又CD⊥平面A1ABB1,则CD⊥A1D,由题意可求出A1D,在Rt△AA1D中,求出AA1,进一步求出FC,则三棱锥F-AEC的体积可求.
解答 (1)证明:如图,∵三棱柱ABC-A1B1C1是直三棱柱,∴AE⊥BB1,
又E是正三角形ABC的边BC的中点,∴AE⊥BC,又BC∩BB1=B,
∴AE⊥平面B1BCC1,而AE?平面AEF,
∴平面AEF⊥平面B1BCC1;
(2)解:∵△ABC是正三角形,∴CD⊥AB,
又三棱柱ABC-A1B1C1是直三棱柱,∴CD⊥AA1,
∴CD⊥平面A1ABB1,则CD⊥A1D,
由题意可知,∠CA1D=30°,∴${A}_{1}D=\sqrt{3}CD=\frac{3}{2}AB=6$.
在Rt△AA1D中,$A{A}_{1}=\sqrt{{A}_{1}{D}^{2}-A{D}^{2}}=4\sqrt{2}$,∴$FC=\frac{1}{2}A{A}_{1}=2\sqrt{2}$.
故三棱锥F-AEC的体积V=$\frac{1}{3}{S}_{△AEC}•FC=\frac{1}{3}×2\sqrt{3}×2\sqrt{2}=\frac{4\sqrt{6}}{3}$.
点评 本题考查了两平面垂直的判定,考查了棱锥的体积,考查了空间想象能力以及计算能力,是中档题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
18.对于平面α和两条不同的直线m、n,下列命题是真命题的是( )
| A. | 若m,n与α所成的角相等,则m∥n | B. | 若m∥α,n∥α,则m∥n | ||
| C. | 若m⊥α,m⊥n,则n∥α | D. | 若m⊥α,n⊥α,则m∥n |
15.设等比数列{an}的公比为q,前n项和为Sn,且a1>0,若S2>2a3,则q的取值范围是( )
| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
12.30岁以后,随着年龄的增长,人们的身体机能在逐渐退化,所以打针 买保健品这样的“健康消费”会越来越多,现对某地区不同年龄段的一些人进行了调查,得到其一年内平均“健康消费”如表:
(1)求“健康消费”y关于年龄x的线性回归方程;
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 |
| 健康消费(百元) | 5 | 8 | 10 | 14 | 18 |
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)