题目内容
20.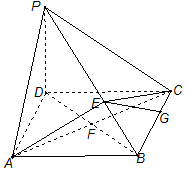 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.(1)求证:AC⊥DE;
(2)当△AEC的面积最小时,求证:CE⊥面PAB
(3)当△AEC的面积最小值为9时,问:线段BC上是否存在点G,使EG与平面PAB所成角的正切值为2?若存在,求出BG的值,若不存在,请说明理由.
分析 (1)连接BD,设AC与BD相交于点F,推导出AC⊥BD,PD⊥AC,从而AC⊥平面PDB,由此能证明AC⊥DE.
(2)连结EF,推导出AC⊥EF,EF⊥PB,PB⊥AC,从而PB⊥平面AEC,进而PB⊥EC,再求出EC⊥AE,由此能证明EC⊥平面PAB.
(3)求出EF=3作GH∥CE交PB于点G,推导出∠GEH就是EG与平面PAB所成角,由此能求出存在满足题意的点G,且BG=4.
解答 证明:(1)连接BD,设AC与BD相交于点F
因为四边形ABCD是菱形,所以AC⊥BD.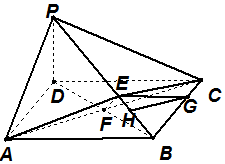
又∵PD⊥平面ABCD,AC?平面ABCD,∴PD⊥AC,
而PD∩BD=D,∴AC⊥平面PDB,
又∵DE?平面PBD,∴AC⊥DE.--------------(4分)
(2)连结EF,由(I)知AC⊥平面PDB,EF?平面PBD,
∴AC⊥EF.∵${S_{△ACE}}=\frac{1}{2}AC•EF$,且AC=6
当△ACE面积最小时,EF最小,这时EF⊥PB.-------(6分)
∵AC⊥平面PDB,∴PB⊥AC,
又∵EF∩AC=F,∴PB⊥平面AEC,∴PB⊥EC,----------------(7分)
又由 EF=AF=FC=3,可得 EC⊥AE,---------(8分)
而PB∩AE=E,
故EC⊥平面PAB.---------------------(9分)
解:(3)由已知,${({{S_{△ACE}}})_{min}}=\frac{1}{2}×6×EF=9$,解得EF=3
作GH∥CE交PB于点G,由(2)知EC⊥平面PAB,
∴GH⊥平面PAB,
∴∠GEH就是EG与平面PAB所成角,----------------------(12分)
在直角三角形CEB中,$BC=6,\;EC=3\sqrt{2}\;,\;EB=3\sqrt{2}$
∴∠CBE=45°
设BG=x,则$BH=HG=\frac{{\sqrt{2}}}{2}x$.
由tan∠GEH=2得 $EH=\frac{{\sqrt{2}}}{4}x$.
由EH+HB=EB得 x=4
即存在满足题意的点G,且BG=4.----------(14分)
点评 本题考查线线垂直的证明,考查线面垂直的证明,考查满足条件的线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
| A. | 20 | B. | 24 | C. | 32 | D. | 40 |
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 |
| 健康消费(百元) | 5 | 8 | 10 | 14 | 18 |
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
| A. | 3 | B. | -3 | C. | $\frac{7}{3}$ | D. | -$\frac{7}{3}$ |
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |