题目内容
5.已知圆C:(x+1)2+(y-2)2=25和点P(2,1)(I)判断点P和圆的位置关系;
(II)过P的直线被圆C截得的弦长为8,求该直线的方程.
分析 (I)求出|PC|,与半径比较,即可判断点P和圆的位置关系;
(II)分类讨论,利用过P的直线被圆C截得的弦长为8,圆心到直线的距离d=3,即可求该直线的方程.
解答 解:(I)∵(2+1)2+(1-2)2=10<25,
∴点P在圆内;
(II)∵过P的直线被圆C截得的弦长为8,
∴圆心到直线的距离d=3,
斜率k不存在时,直线方程为x=2,满足题意;
斜率存在时,设方程为y-1=k(x-2),即kx-y-2k+1=0,
圆心到直线的距离d=$\frac{|-k-2-2k+1|}{\sqrt{{k}^{2}+1}}$=3,解得k=-$\frac{4}{3}$,
∴直线方程为4x+3y-11=0,
综上所述,直线的方程为x=2或4x+3y-11=0.
点评 本题考查点与圆、直线与圆的位置关系,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设等比数列{an}的公比为q,前n项和为Sn,且a1>0,若S2>2a3,则q的取值范围是( )
| A. | $(-1,0)∪(0,\frac{1}{2})$ | B. | $(-\frac{1}{2},0)∪(0,1)$ | C. | $(-1,\frac{1}{2})$ | D. | $(-\frac{1}{2},1)$ |
20.已知点F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点,点B是短轴顶点,直线BF2与椭圆C相交于另一点D.若△F1BD是等腰三角形,则椭圆C的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
10.已知集合M={0,1,2,3,4},N={2,4,6},P=M∩N,则P的子集有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
14.已知O为正△ABC内的一点,且满足$\overrightarrow{OA}+λ\overrightarrow{OB}+(1+λ)\overrightarrow{OC}=\overrightarrow 0$,若△OAB的面积与△OBC的面积的比值为3,则λ的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
15.已知集合$A=\{x|x<2\},B=\{x|\frac{x}{x-1}<1\},R$为实数集,则集合A∩(∁RB)=( )
| A. | R | B. | (-∞,2) | C. | (1,2) | D. | [1,2) |
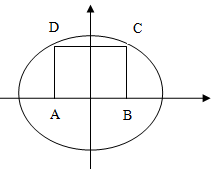 如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.
如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.