题目内容
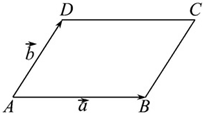如图，?ABCD中，| AB |
| a |
| AD |
| b |
（1）当
| a |
| b |
| a |
| b |
| a |
| b |
（2）当
| a |
| b |
| a |
| b |
| a |
| b |
（3）
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）利用菱形的对角线的性质即可得出；
（2）利用矩形的对角线的性质即可得出；
（3）利用平行四边形的对角线的性质即可判断出．
（2）利用矩形的对角线的性质即可得出；
（3）利用平行四边形的对角线的性质即可判断出．
解答：
解：（1）易知
+
=
，
-
=
．
表示
+
与
-
的有向线段所在的直线垂直，
即AC⊥BD．
又∵四边形ABCD为平行四边形，
∴四边形ABCD为菱形，即
、
应满足|
|=|
|．
（2）|
+
|=|
-
|，即|
|=|
|．
∵矩形的对角线相等．
∴当表示
，
的有向线段所在的直线垂直时，
满足|
+
|=|
-
|．
（3）不可能，因为□ABCD的两条对角线不可能平行，因此
+
与
-
不可能为共线向量，那么就不可能为相等向量了．
| a |
| b |
| AC |
| a |
| b |
| DB |
表示
| a |
| b |
| a |
| b |
即AC⊥BD．
又∵四边形ABCD为平行四边形，
∴四边形ABCD为菱形，即
| a |
| b |
| a |
| b |
（2）|
| a |
| b |
| a |
| b |
| AC |
| DB |
∵矩形的对角线相等．
∴当表示
| a |
| b |
满足|
| a |
| b |
| a |
| b |
（3）不可能，因为□ABCD的两条对角线不可能平行，因此
| a |
| b |
| a |
| b |
点评：本题考查了菱形的对角线的性质、矩形的对角线的性质、平行四边形的对角线的性质、向量的平行四边形法则，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知四边形OABC与OADE是两个全等的矩形，M，N分别是OD与AC上两点，且OM=AN，过M作MM1∥OA交OE于点M1，连接M1N．
如图，四棱锥P-ABCD的底面ABCD是直角梯形，AD∥BC，AB⊥BC，平面PAB⊥底面ABCD，PA=AD=AB=1，BC=2．