题目内容
已知函数f(x)=lnx-x
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若不等式af(x)≥x-
x2在x∈(0,+∞)内恒成立,求实数a的取值范围;
(Ⅲ)n∈N*,求证:
+
+…+
>
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若不等式af(x)≥x-
| 1 |
| 2 |
(Ⅲ)n∈N*,求证:
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| ln(n+1) |
| n |
| n+1 |
考点:函数恒成立问题
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,利用导数的正负,可求f(x)的单调区间;
(Ⅱ)af(x)≥x-
x2即Q(x)=
x2+aInx-(a+1)x≥o成立,求导数,分类讨论,求出函数的最小值,即可求实数a的取值范围;
(Ⅲ)先证明lnx≤x2-x(x=1取等号),可得当x>1时,
>
=
=
-
,令x=2,3,4,…,相加可得结论.
(Ⅱ)af(x)≥x-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)先证明lnx≤x2-x(x=1取等号),可得当x>1时,
| 1 |
| lnx |
| 1 |
| x2-x |
| 1 |
| (x-1)x |
| 1 |
| x-1 |
| 1 |
| x |
解答:
解:(I)∵f(x)=lnx-x,
∴f′(x)=
,
∴f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞);---------------(4分)
(II)af(x)≥x-
x2即Q(x)=
x2+aInx-(a+1)x≥o成立,
Q′(x)=x+
-(a+1)=
①若a≤0时,Q'(x)在(0,1)小于0,Q(x)递减;Q'(x)在(1,+∞)大于0,Q(x)递增
∴Q(1)=
-(a+1)≥0,解得a≤-
,
又a≤0,故a≤-
②若0<a≤1时,Q'(x)=0解得x=a或x=1,列表如下
又Q(1)=
-(a+1)<0,故不满足要求
③若a>1时,Q'(x)=0解得x=a或x=1,列表如下
同理Q(1)=
-(a+1)<0,故也不满足要求
综合上述,要使不等式af(x)≥x-
x2在x∈(0,+∞)内恒成立,则实数a的取值范围为a∈(-∞,-
]-------------------(10分)
( III)由( II)知当a=-
时,Q(x)=
x2-
Inx-
x≥o
即lnx≤x2-x(x=1取等号)
∴当x>1时,
>
=
=
-
令x=2,3,4,…,则有
>1-
,
>
-
,
>
-
,…,
>
-
相加得
+
+…+
>1-
+
-
+…
-
=1-
=
--------(14分)
∴f′(x)=
| 1-x |
| x |
∴f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞);---------------(4分)
(II)af(x)≥x-
| 1 |
| 2 |
| 1 |
| 2 |
Q′(x)=x+
| a |
| x |
| (x-a)(x-1) |
| x |
①若a≤0时,Q'(x)在(0,1)小于0,Q(x)递减;Q'(x)在(1,+∞)大于0,Q(x)递增
∴Q(1)=
| 1 |
| 2 |
| 1 |
| 2 |
又a≤0,故a≤-
| 1 |
| 2 |
②若0<a≤1时,Q'(x)=0解得x=a或x=1,列表如下
| x | (0,a) | a | (a,1) | 1 | (1,+∞) |
| Q'(x) | + | 0 | - | 0 | + |
| Q(x) | 增 | 减 | 增 |
| 1 |
| 2 |
③若a>1时,Q'(x)=0解得x=a或x=1,列表如下
| x | (0,1) | 1 | (1,a) | a | (a,+∞) |
| Q'(x) | + | 0 | - | 0 | + |
| Q(x) | 增 | 减 | 增 |
| 1 |
| 2 |
综合上述,要使不等式af(x)≥x-
| 1 |
| 2 |
| 1 |
| 2 |
( III)由( II)知当a=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即lnx≤x2-x(x=1取等号)
∴当x>1时,
| 1 |
| lnx |
| 1 |
| x2-x |
| 1 |
| (x-1)x |
| 1 |
| x-1 |
| 1 |
| x |
令x=2,3,4,…,则有
| 1 |
| ln2 |
| 1 |
| 2 |
| 1 |
| ln3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| ln4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| ln(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
相加得
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| ln(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查函数恒成立问题,考查函数的单调性,考查不等式的证明,正确求导是关键.

练习册系列答案
相关题目
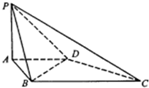 如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.
如图,四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,AB⊥BC,平面PAB⊥底面ABCD,PA=AD=AB=1,BC=2.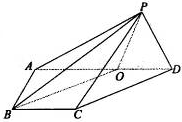 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.