题目内容
9．把89化成四进制数的末位数字为1．分析 利用“除k取余法”是将十进制数除以4，然后将商继续除以4，直到商为0，然后将依次所得的余数倒序排列即可得到答案．
解答 解：89÷4=22…1
22÷4=5…2
5÷4=1…1
1÷4=0…1
故89（10）=1121（4）
可得末位数字为1．
故答案为：1．
点评 本题考查的知识点是十进制与其它进制之间的转化，其中熟练掌握“除k取余法”的方法步骤是解答本题的关键，属于基础题．
练习册系列答案
相关题目
19．已知直线l与双曲线$\frac{x^2}{4}-{y^2}=1$相切于点P，l与双曲线两条渐进线交于M，N两点，则$\overrightarrow{OM}•\overrightarrow{ON}$的值为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 与P的位置有关 |
4．2016年美国总统大选过后，有媒体从某公司的全体员工中随机抽取了200人，对他们的投票结果进行了统计（不考虑弃权等其他情况），发现支持希拉里的一共有95人，其中女员工55人，支持特朗普的男员工有60人．
（Ⅰ）根据已知条件完成下面的2×2列联表：据此材料，是否有95%的把握认为投票结果与性别有关？
（Ⅱ）若从该公司的所有男员工中随机抽取3人，记其中支持特朗普的人数为X，求随机变量X的分布列和数学期望．（用相应的频率估计概率）
附：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
（Ⅰ）根据已知条件完成下面的2×2列联表：据此材料，是否有95%的把握认为投票结果与性别有关？
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
附：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
14．如果有95%的把握说事件A和B有关，那么具体算出的数据满足（ ）
| A． | K 2＞3.841 | B． | K 2＜3.841 | C． | K 2＞6.635 | D． | K 2＜6.635 |
1．已知函数f（x）=cos（2x+φ），且${∫}_{0}^{\frac{2}{3}π}$f（x）dx=0，则下列说法正确的是（ ）
| A． | f（x）的一条对称轴为x=$\frac{5π}{12}$ | |
| B． | 存在φ使得f（x）在区间[-$\frac{π}{6}$，$\frac{π}{3}$]上单调递减 | |
| C． | f（x）的一个对称中心为（$\frac{5π}{12}$，0） | |
| D． | 存在φ使得f（x）在区间[$\frac{π}{12}$，$\frac{7π}{12}$]上单调递增 |
19．
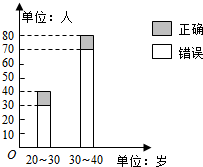“开门大吉”是某电视台推出的游戏节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关；说明你的理由：（下面的临界值表供参考）
（Ⅱ）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
“开门大吉”是某电视台推出的游戏节目，选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金，在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关；说明你的理由：（下面的临界值表供参考）
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）