题目内容
4. 为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )
为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
分析 先分别求出中位数和平均数,由此能求出结果.
解答 解:平均数$\overline{x}$=$\frac{1}{10}(41+44+50+53+56+60+61+62+70)=54$.8,
中位数为:$\frac{1}{2}(53+56)=54.5$,
∴这10位学生体重的平均数与中位数之差为:
54.8-54.5=0.3.
故选:C.
点评 本题考查一组数据的平均数和中位数之差的求法,是基础题,解题时要认真审题,注意茎叶图的合理运用.

练习册系列答案
相关题目
14.某研究机构对高二学生的记忆力x和判断力y进行统计分析,给出变量x、y的6组数据如表:
由表中数据得出线性回归方程y=$\widehat{b}$x+$\widehat{a}$的斜率为$\widehat{b}$=3.3.当x=12时,预测y的值为( )
| x | 3 | 4 | 5 | 6 | 8 | 10 |
| y | 40 | 45 | 60 | 55 | 70 | 90 |
| A. | 79.8 | B. | 96.6 | C. | 83.1 | D. | 69.7 |
12.若集合M={x|x>2},n={x|1<x≤3},则N∩(∁RM)等于( )
| A. | (1,2] | B. | [-2,2] | C. | (1,2) | D. | [2,3] |
19.已知函数y=xln(1+x2),则函数y的极值情况是( )
| A. | 有极小值 | B. | 有极大值 | ||
| C. | 既有极大值又有极小值 | D. | 无极值 |
9.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2014}$的值的一个程序框图,则判断框内可填入的条件是( )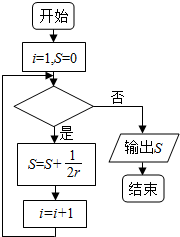

| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
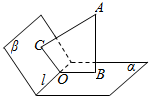 如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.
如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.