题目内容
12.直线x•(2t-1)-y(2t+1)+1=0(t∈R)的倾斜角为α,则α的范围是( )| A. | 0≤α<$\frac{π}{4}$或$\frac{3π}{4}$<α≤π | B. | $\frac{π}{4}$≤α≤$\frac{3π}{4}$且α≠$\frac{π}{2}$ | C. | 0≤α<$\frac{π}{4}$或$\frac{3π}{4}$<α<π | D. | 0≤α<$\frac{π}{4}$ |
分析 根据倾斜角、斜率的定义得到tanα=$\frac{{2}^{t}-1}{{2}^{t}+1}$,结合函数的性质进行解答.
解答 解:∵直线x•(2t-1)-y(2t+1)+1=0(t∈R)的倾斜角为α,
∴tanα=$\frac{{2}^{t}-1}{{2}^{t}+1}$=1-$\frac{2}{{2}^{t}+1}$,
∵y=2t+1>1,
∴0<$\frac{2}{{2}^{t}+1}$<2,
∴-1<1-$\frac{2}{{2}^{t}+1}$<1,
∴0≤α<$\frac{π}{4}$或$\frac{3π}{4}$<α<π.
故选:C.
点评 本题考查了直线斜率的求法,考查了斜率和倾斜角的关系,是基础题.

练习册系列答案
相关题目
3.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+ax-b(x>0)}\\{0(x=0)}\\{g(x)(x<0)}\end{array}\right.$在区间(a+$\frac{4}{a}$,-b2+4b)上满足f(-x)+f(x)=0,则g(-$\sqrt{2}$)的值为( )
| A. | -2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
4.设a=30.4,b=log30.4,c=0.43,则a,b,c的大小关系为( )
| A. | a>c>b | B. | a>b>c | C. | c>a>b | D. | c>b>a |
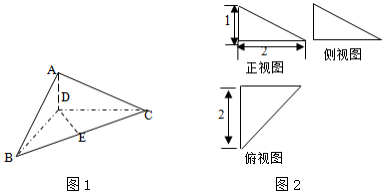
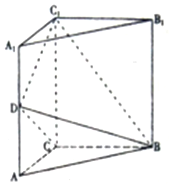 如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=$\frac{1}{2}A{A_1}$=2,点D是棱AA1的中点.