题目内容
9.已知函数g(x)=ex(x+1).(1)求函数g(x)在(0,1)处的切线方程;
(2)设x>0,讨论函数h(x)=g(x)-a(x3+x2)(a>0)的零点个数.
分析 (1)求导数,确定切线的斜率,即可求函数g(x)在(0,1)处的切线方程;
(2)h(x)=g(x)-a(x3+x2)=0,可得a=$\frac{{e}^{x}}{{x}^{2}}$,确定函数的单调性,可得函数的极小值,即可得出结论.
解答 解:(1)g′(x)=ex(x+2),g′(0)=2,
∴函数g(x)在(0,1)处的切线方程为y-1=2x,即l:y=2x+1(4分)
(2)h(x)=g(x)-a(x3+x2)=0,可得a=$\frac{{e}^{x}}{{x}^{2}}$,
设y=$\frac{{e}^{x}}{{x}^{2}}$,则y′=$\frac{{e}^{x}(x-2)}{{x}^{3}}$,函数在(0,2)上单调递减,(2,+∞)上单调递增,
∴x=2函数取得极小值$\frac{{e}^{2}}{4}$,
∴$a=\frac{e^2}{4}$,零点1个; $a>\frac{e^2}{4}$,零点2个;$0<a<\frac{e^2}{4}$,零点0个 (8分)
点评 本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性的运用,属于中档题.

练习册系列答案
相关题目
19.已知函数$f(x)=\frac{{\sqrt{3}}}{2}sin2x+{cos^2}x-\frac{1}{2}$,若将其图象向左平移φ(φ>0)个单位后所得的图象关于原点对称,则φ的最小值为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{7π}{12}$ | C. | $\frac{5π}{12}$ | D. | $\frac{π}{12}$ |
20.若${(3x-\frac{1}{{\sqrt{x}}})^n}(n∈N*)$的展开式中各项系数和为64,则其展开式中的常数项为( )
| A. | 540 | B. | -540 | C. | 135 | D. | -135 |
17.已知函数$f(x)=\left\{\begin{array}{l}f(x+1),x<4\\{2^x},x≥4\end{array}\right.$,则f(2+log23)=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 24 |
18.已知等差数列{an}的前项和为Sn,且S5=30,则a3=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.在△ABC上,点D满足$\overrightarrow{AD}=2\overrightarrow{AB}-\overrightarrow{AC}$,则( )
| A. | 点D不在直线BC上 | B. | 点D在BC的延长线上 | ||
| C. | 点D在线段BC上 | D. | 点D在CB的延长线上 |
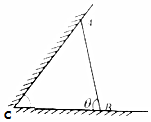 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ