题目内容
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(3,2),当a2+b2取得最小值时,椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 将点代入椭圆方程,利用“1”代换,根据基本不等式的即可a和b的关系,利用椭圆的离心率即可求得
解答 解:由点在椭圆上则:$\frac{9}{{a}^{2}}+\frac{4}{{b}^{2}}=1$,则a2+b2=(a2+b2)($\frac{9}{{a}^{2}}$+$\frac{4}{{b}^{2}}$)=9+$\frac{4{a}^{2}}{{b}^{2}}$+$\frac{9{b}^{2}}{{a}^{2}}$+4≥13+2$\sqrt{\frac{4{a}^{2}}{{b}^{2}}•\frac{9{b}^{2}}{{a}^{2}}}$≥25,
当且仅当$\frac{4{a}^{2}}{{b}^{2}}$=$\frac{9{b}^{2}}{{a}^{2}}$,即$\frac{{b}^{2}}{{a}^{2}}$=$\frac{2}{3}$,
由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{3}$,
∴椭圆的离心率$\frac{\sqrt{3}}{3}$,
故选:D.
点评 本题考查椭圆的方程及椭圆的离心率,考查“1”代换,基本不等式的性质,考查转化思想,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
9.定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x∈[0,1)}\\{-(\frac{1}{2})^{|x-\frac{3}{2}|}x∈[1,2)}\end{array}\right.$,若当x∈[-4,-2)时,不等式f(x)≥$\frac{{t}^{2}}{4}$-t+$\frac{1}{2}$恒成立,则实数t的取值范围是( )
| A. | [2,3] | B. | [1,3] | C. | [1,4] | D. | [2,4] |
9.等比数列{an}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2,a4=16,则S4=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
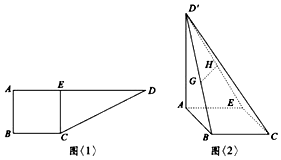 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.