题目内容
15.已知向量$\vec a$与$\vec b$的夹角为$\frac{2π}{3}$,$|\vec a|=\sqrt{2}$,则$\vec a$在$\vec b$方向上的投影为$-\frac{\sqrt{2}}{2}$.分析 由条件,可得出$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为$|\overrightarrow{a}|cos\frac{2π}{3}$,从而求出投影的值.
解答 解:根据条件,$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影为:
$|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>=\sqrt{2}cos\frac{2π}{3}=-\frac{\sqrt{2}}{2}$.
故答案为:$-\frac{\sqrt{2}}{2}$.
点评 考查向量夹角的概念,向量投影的概念及计算公式.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
3.已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,取DE的中点F,则$\overrightarrow{AF}•\overrightarrow{BC}$的值为( )
| A. | $-\frac{5}{8}$ | B. | $-\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | $\frac{11}{8}$ |
20.若${(3x-\frac{1}{{\sqrt{x}}})^n}(n∈N*)$的展开式中各项系数和为64,则其展开式中的常数项为( )
| A. | 540 | B. | -540 | C. | 135 | D. | -135 |
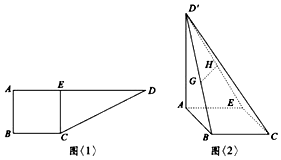 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.