题目内容
已知△ABC的三个内角A、B、C，向量
=（sinA，1），
=（1，-
cosA），且
⊥
．则角A= ．
| m |
| n |
| 3 |
| m |
| n |
考点：平面向量数量积的运算
专题：计算题,三角函数的求值,平面向量及应用
分析：运用向量垂直的条件：数量积为0，再由同角的商数关系，计算即可得到所求值．
解答：
解：由
=（sinA，1），
=（1，-
cosA），且
⊥
，
则
•
=0，
即有sinA-
cosA=0，
即tanA=
=
，
由于A为三角形的内角，
则A=
．
故答案为：
．
| m |
| n |
| 3 |
| m |
| n |
则
| m |
| n |
即有sinA-
| 3 |
即tanA=
| sinA |
| cosA |
| 3 |
由于A为三角形的内角，
则A=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查向量的数量积的坐标表示和向量垂直的条件：数量积为0，同时考查同角的商数关系，属于基础题．
练习册系列答案
相关题目
如图所示，动物园要建造2间面积相同的矩形动物居室，如果可供建造围墙的材料总长是24m，设这两间动物居室的宽为x（单位：m），两间动物居室总面积为y（单位：m2），（注：围墙的厚度忽略不计）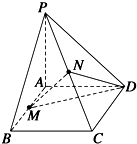
如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，M，N分别是AB、PC的中点