题目内容
掷一颗质地均匀的骰子，观察所得的点数a，设事件A=“a为3”，B=“a为4”，C=“a为奇数”，则下列结论正确是（ ）
| A、A与B为互斥事件 |
| B、A与B为对立事件 |
| C、A与C为对立事件 |
| D、A与C为互斥事件 |
考点：互斥事件与对立事件
专题：概率与统计
分析：观察所给的三个事件，A与B是互斥事件，B与C是互斥事件，这里没有对立事件，A事件包含在C事件里，得到结论．
解答：
解：∵设事件A=“a为3”，B=“a为4”，C=“a为奇数”，
∴A与B是互斥事件，
B与C是互斥事件，
这里没有对立事件，
A事件包含在C事件里，
故选：A．
∴A与B是互斥事件，
B与C是互斥事件，
这里没有对立事件，
A事件包含在C事件里，
故选：A．
点评：本题考查互斥事件与对立事件，本题解题的关键是看出所给的三个事件之间的关系，注意理解对立事件与互斥事件之间的关系，本题是一个基础题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知定义在R上的函数f（x），其导函数y=f′（x）的大致图象如图所示，则下列叙述正确的是（ ）| A、f（a）取得极小值 |
| B、f（d）取得最小值 |
| C、f（x）在（a，c）上单调递增 |
| D、f（e）取得极大值 |
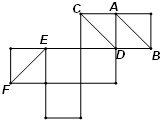如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（ ）| A、AB∥CD，EF⊥CD |
| B、AB与CD异面成角60°，CD与EF相交成角60° |
| C、AB∥CD，CD与EF相交成角60° |
| D、EF⊥CD，AB与CD异面成角60° |
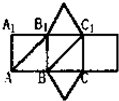如图，正三棱柱的平面展开图，各侧面都是正方形，在这个正三棱柱中：①AB1∥BC1；
②AC1与BC是异面直线；
③AB1与BC所成的角的余弦值为
| ||
| 4 |
④BC1与A1C垂直．
其中正确的是（ ）
| A、①③ | B、②③ | C、②④ | D、②③④ |
函数f（x）=x2-ax+2在（2，+∞）上单调递增，则a的取值范围为（ ）
| A、[2，+∞） |
| B、[4，+∞） |
| C、（-∞，4] |
| D、（-∞，-4] |
函数f（x）=x2-x的零点个数是（ ）
| A、3 | B、2 | C、1 | D、0 |
函数f（x）=lg
的图象（ ）
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |