Question

过双曲线

x2

a2

-

y2

b2

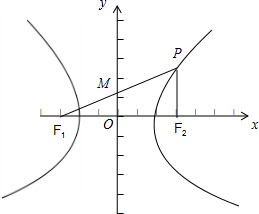
=1(a＞0，b＞0)左焦点F₁且倾斜角为45°的直线交双曲线右支于点P，若线段PF₁的中点Q落在y轴上，则此双曲线的离心率为（　　）

• A、

  3

• B、1+

  3

• C、

  2

• D、1+

  2

Answer 1

考点：双曲线的简单性质

专题：综合题,圆锥曲线的定义、性质与方程

分析：设F₁（-c，0），P（x₀，y₀），依题意可求得直线PF₁的方程为：y=x+c，△MF₁O为直角三角形，经分析知OM为直角三角形PF₁F₂的中位线，从而可求得|PF₁|与|PF₂|，利用双曲线定义及离心率公式即可求得答案．

解答： 解：设F₁（-c，0），P（x₀，y₀），
依题意，直线PF₁的方程为：y=x+c，
设直线PF₁与y轴的交点为M（0，m），
∵M为线段PF₁的中点，
∴

x0-c

2

=0，m=

y0

2

．
∴x₀=c，
∴y₀=x₀+c=2c，m=c．
∵△MF₁O为直角三角形，∠PF₁O=45°，
∴|MF₁|=

2

|OM|=

2

c；
又M为线段PF₁的中点，O为F₁F₂的中点，
∴OM为直角三角形PF₁F₂的中位线，
∴|PF₁|=2

2

c，|PF₂|=2c，
∴2a=|PF₁|-|PF₂|=（2

2

-2）c，
∴其离心率e=

c

a

=1+

2

．
故选：D．

点评：本题考查双曲线的简单性质，着重考查双曲线的定义，求得|PF₁|与|PF₂|是关键，考查作图、分析、与运算能力，属于中档题．