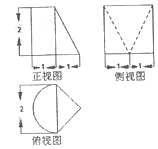
题目内容
11.一个圆锥与一个球的体积相等,圆锥的底面半径是球半径的3倍,圆锥的高与球半径之比为$\frac{4}{9}$.分析 根据球和圆锥的体积公式列方程化简即可得出结论.
解答 解:设球的半径为r,则圆锥的底面半径为3r,圆锥的高为h,
则$\frac{1}{3}π•(3r)^{2}h$=$\frac{4π{r}^{3}}{3}$,
∴h=$\frac{4r}{9}$,即$\frac{h}{r}$=$\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题考查了几何体的体积公式,属于基础题.

练习册系列答案
相关题目
19.用0,1,2,3,4,5这6个数,能组成几个没有重复数字的四位偶数( )
| A. | 18 | B. | 156 | C. | 192 | D. | 360 |
3.已知$α,β∈({0,\frac{π}{,2}})$,下列不等式中不成立的是( )
| A. | sinα+cosα>1 | B. | sinα-cosα<1 | C. | cos(α+β)>cos(α-β) | D. | sin(α+β)>sin(α-β) |
20.“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是$\frac{8}{15}$.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为X,求X的分布列、数学期望.
| 男性 | 女性 | 总计 | |
| 爱好 | 10 | ||
| 不爱好 | 8 | ||
| 总计 | 30 |
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为X,求X的分布列、数学期望.