题目内容
1.某班主任对全班40名学生进行了作业量多少的调查.数据如下表:| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩游戏 | 20 | 10 | |
| 不喜欢玩游戏 | 2 | 8 | |
| 总计 |
(Ⅱ)根据表中数据,问是否有95%的把握认为“喜欢玩游戏与作业量的多少有关系”?
| P(x2≥k) | 0.100 0.050 0.010 |
| k | 2.706 3.841 6.635 |
分析 (Ⅰ)根据题意填写列联表即可;
(Ⅱ)计算观测值,对照临界值得出结论.
解答 解:(Ⅰ)填写列联表,如下;
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩游戏 | 20 | 10 | 30 |
| 不喜欢玩游戏 | 2 | 8 | 10 |
| 总计 | 22 | 18 | 40 |
(Ⅱ)将表中的数据代入公式:
χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{(n}_{11}{+n}_{12}){(n}_{21}{+n}_{22}){(n}_{11}{+n}_{21}){(n}_{12}{+n}_{22})}$,
得x2=$\frac{40(20×8-2×10)^{2}}{22×18×10×30}$,…(10分)
计算得χ2≈6.599>3.841,
所以有95%把握认为喜欢玩游戏与作业量的多少有关系…(12分)
点评 本题考查了列联表与独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
13.设x,y满足约束条件$\left\{\begin{array}{l}{2x+y-5≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,若z=ax+y仅在点(2,1)处取得最大值,则a的取值范围是( )
| A. | (-∞,-1) | B. | (2,+∞) | C. | (0,2) | D. | (-1,+∞) |
14.下列函数中,在定义域上为减函数的是( )
| A. | y=x2 | B. | y=cosx | C. | $y={x^{\frac{1}{2}}}$ | D. | y=-lnx |
10.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )
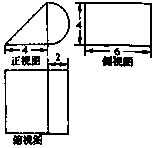

| A. | 24+6πcm3 | B. | 24+12πcm3 | C. | 48+12πcm3 | D. | 96+12πcm3 |
11.已知向量$\overrightarrow a≠\overrightarrow e$,$|\overrightarrow e|=1$,对任意t∈R,恒有$|\overrightarrow a-t\overrightarrow e|≥|\overrightarrow a-2\overrightarrow e|$,则( )
| A. | $\overrightarrow a⊥\overrightarrow e$ | B. | $\overrightarrow a⊥(\overrightarrow a-2\overrightarrow e)$ | C. | $\overrightarrow e⊥(\overrightarrow a-2\overrightarrow e)$ | D. | $(\overrightarrow a+2\overrightarrow e)⊥(\overrightarrow a-2\overrightarrow e)$ |