题目内容
 如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=
如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=| 1 |
| 2 |
(1)求面MNC与面NCB所成的锐二面角的余弦值.
(2)在线段PA(包括端点)上是否存在一点Q,使SQ⊥平面MNC?若存在,确定Q的位置;若不存在,说明理由.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:计算题,空间位置关系与距离,空间角
分析:建立空间直角坐标系,利用向量法分别证明直线垂直,求二面角的大小即可.
解答:
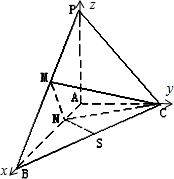 解:(1)以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图,
解:(1)以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图,
则M(2,0,1),N(1,0,0),C(0,2,0),B(4,0,0),P(0,0,2),S(2,1,0),
∴
=(-1,0,-1),
=(-1,2,0),
设面MNC的法向量为
=(x,y,z),则
,
∴
=(2,1,-2),
∵面NCB的法向量为
=(0,0,2),
∴面MNC与面NCB所成的锐二面角的余弦值为|
=
;
(2)设Q(0,0,c)(0≤c≤2),则
=(-2,-1,c),
若SQ⊥平面MNC,则
∥
,∴c=2,
即Q为P点时,SQ⊥平面MNC.
 解:(1)以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图,
解:(1)以A为原点,射线AB,AC,AP分别为x,y,z轴正向建立空间直角坐标系如图,则M(2,0,1),N(1,0,0),C(0,2,0),B(4,0,0),P(0,0,2),S(2,1,0),
∴
| MN |
| NC |
设面MNC的法向量为
| n |
|
∴
| n |
∵面NCB的法向量为
| m |
∴面MNC与面NCB所成的锐二面角的余弦值为|
| 4 | ||
|
| 2 |
| 3 |
(2)设Q(0,0,c)(0≤c≤2),则
| SQ |
若SQ⊥平面MNC,则
| SQ |
| n |
即Q为P点时,SQ⊥平面MNC.
点评:本题主要考查空间位置关系的判断,以及空间二面角和的大小求法,建立空间直角坐标系,利用向量坐标法是解决此类问题比较简洁的方法.

练习册系列答案
相关题目
在调查高中学生的近视情况中,某校高一年级145名男生中有60名近视,120名女生中有70名近视.在检验这些高中学生眼睛近视是否与性别相关时,常采用的数据分析方法是( )
| A、期望与方差 | B、独立性检验 |
| C、正态分布 | D、二项分布列 |
 已知四棱锥P-ABCD,四边形ABCD为矩形,且PA⊥ABCD,E,F是PB的三等分点,E,F在PB上,PA=12,DC=9,BD=5,求异面直线DE与CF的夹角.
已知四棱锥P-ABCD,四边形ABCD为矩形,且PA⊥ABCD,E,F是PB的三等分点,E,F在PB上,PA=12,DC=9,BD=5,求异面直线DE与CF的夹角.