题目内容
已知动点M到定点(1,0)的距离比M到定直线x=-2的距离小1.
(Ⅰ)求点M的轨迹曲线C的方程;
(Ⅱ)大家知道,过圆上任意一点P,任意作两条相互垂直的弦PA,PB,则弦AB必过圆心(定点),受此启发,过曲线C上一点P,任意作两条相互垂直的弦PA,PB.
(ⅰ)若点P恰好是曲线C的顶点,则弦AB是否经过一个定点?若经过定点(设为Q),请求出Q点的坐标,否则说明理由;
(ⅱ)试探究:若改变曲线C的开口,且点P不是曲线C的顶点,(ⅰ)中的结论是否仍然成立?若成立,请给出一个使(ⅰ)中的结论成立的命题,并加以证明,否则说明理由.
(Ⅰ)求点M的轨迹曲线C的方程;
(Ⅱ)大家知道,过圆上任意一点P,任意作两条相互垂直的弦PA,PB,则弦AB必过圆心(定点),受此启发,过曲线C上一点P,任意作两条相互垂直的弦PA,PB.
(ⅰ)若点P恰好是曲线C的顶点,则弦AB是否经过一个定点?若经过定点(设为Q),请求出Q点的坐标,否则说明理由;
(ⅱ)试探究:若改变曲线C的开口,且点P不是曲线C的顶点,(ⅰ)中的结论是否仍然成立?若成立,请给出一个使(ⅰ)中的结论成立的命题,并加以证明,否则说明理由.
考点:直线与圆锥曲线的关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用抛物线的定义,可求点M的轨迹曲线C的方程;
(Ⅱ)(i)求出A,B的坐标,可得直线AB的方程,令y=0,可得直线AB必过定点Q(4,0);
(ⅱ)过抛物线y2=2px上顶点以外的定点P任作两条相互垂直的弦PA,PB,则弦AB必过定点.假设AB过定点Q(a,b),
=
化简得y1y2-b(y1+y2)+2pa=0,即可得出结论.
(Ⅱ)(i)求出A,B的坐标,可得直线AB的方程,令y=0,可得直线AB必过定点Q(4,0);
(ⅱ)过抛物线y2=2px上顶点以外的定点P任作两条相互垂直的弦PA,PB,则弦AB必过定点.假设AB过定点Q(a,b),
| y1-b | ||
|
| y2-b | ||
|
解答:
解:(Ⅰ)M到定点(1,0)的距离等于到定直线x=-1的距离,
∴轨迹为抛物线…(2分)
轨迹方程为y2=4x…(3分)
(Ⅱ)(i)依题意得设OA:y=kx,(k≠0),此时OB:y=-
x
由
得A(
,
),…(5分)
同理B(4k2,-4k)…(6分)
因此AB方程为y+4k=
(x-4k2)
即y+4k=
(x-4k2)…(7分)
令y=0得4k(
-k)=x-4k2,∴x=4,
∴直线AB必过定点Q(4,0)…(8分)
(ii)结论:过抛物线y2=2px上顶点以外的定点P任作两条相互垂直的弦PA,PB,则弦AB必过定点.
设点P(x0,y0)为y2=2px上一定点(非原点),则y02=2px0
过P作互相垂直的弦PA,PB
设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
∴
•
=-1,
∴
•
=-1,
化简得(y1+y0)(y2+y0)=-4p2即y1y2+y0(y1+y2)+y02+4p2=0(*)…(10分)
假设AB过定点Q(a,b),则有
=
即
=
化简得y1y2-b(y1+y2)+2pa=0(**)…(12分)
比较(*)、(**)得a=2p+x0,b=-y0,
∴过定点Q(x0+2p,-y0)…(13分)
∴轨迹为抛物线…(2分)
轨迹方程为y2=4x…(3分)
(Ⅱ)(i)依题意得设OA:y=kx,(k≠0),此时OB:y=-
| 1 |
| k |
由
|
| 4 |
| k2 |
| 4 |
| k |
同理B(4k2,-4k)…(6分)
因此AB方程为y+4k=
| ||
|
即y+4k=
| 1 | ||
|
令y=0得4k(
| 1 |
| k |
∴直线AB必过定点Q(4,0)…(8分)
(ii)结论:过抛物线y2=2px上顶点以外的定点P任作两条相互垂直的弦PA,PB,则弦AB必过定点.
设点P(x0,y0)为y2=2px上一定点(非原点),则y02=2px0
过P作互相垂直的弦PA,PB
设A(x1,y1),B(x2,y2),则y12=2px1,y22=2px2,
∴
| y1-y0 |
| x1-x0 |
| y2-y0 |
| x2-x0 |
∴
| y1-y0 | ||||
|
| y2-y0 | ||||
|
化简得(y1+y0)(y2+y0)=-4p2即y1y2+y0(y1+y2)+y02+4p2=0(*)…(10分)
假设AB过定点Q(a,b),则有
| y1-b |
| x1-a |
| y2-b |
| x2-a |
即
| y1-b | ||
|
| y2-b | ||
|
比较(*)、(**)得a=2p+x0,b=-y0,
∴过定点Q(x0+2p,-y0)…(13分)
点评:本题主要考查抛物线的标准方程,直线与圆锥曲线的位置关系等基础知识,考查推理论证能力,运算求解能力及创新意识,考查化归与转化思想,数形结合思想以及特殊与一般思想.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=
如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=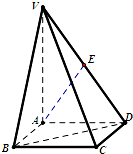 如图,在四棱锥V-ABCD中,VA⊥底面ABCD,底面ABCD是边长为2的正方形.
如图,在四棱锥V-ABCD中,VA⊥底面ABCD,底面ABCD是边长为2的正方形.