题目内容
已知α、β是方程x2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a、b∈R,求2a+3b的最大值和最小值.
考点:不等关系与不等式
专题:不等式的解法及应用
分析:令f(x)=x2+ax+2b,由于α、β是方程x2+ax+2b=0的两根,且α∈[0,1],β∈[1,2],a、b∈R,可得
,画出可行域,设目标函数l:2a+3b=m,则b=-
a+
.利用斜率的意义即可得出最值.
|
| 2 |
| 3 |
| m |
| 3 |
解答:
解:令f(x)=x2+ax+2b,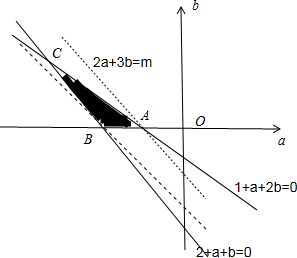
∵α、β是方程x2+ax+2b=0的两根,
且α∈[0,1],β∈[1,2],a、b∈R,
∴
画出可行域:
可得A(-1,0),B(-2,0).
设目标函数l:2a+3b=m,则b=-
a+
.
由斜率的意义可知:当直线l经过点A(-1,0)时,m取得最大值,m=-2.
当直线l经过点B(-2,0)时,m取得最小值,m=-4.
∴2a+3b的最大值为-2,最小值为-4.

∵α、β是方程x2+ax+2b=0的两根,
且α∈[0,1],β∈[1,2],a、b∈R,
∴
|
画出可行域:
可得A(-1,0),B(-2,0).
设目标函数l:2a+3b=m,则b=-
| 2 |
| 3 |
| m |
| 3 |
由斜率的意义可知:当直线l经过点A(-1,0)时,m取得最大值,m=-2.
当直线l经过点B(-2,0)时,m取得最小值,m=-4.
∴2a+3b的最大值为-2,最小值为-4.
点评:本题综合考查了一元二次方程、线性规划的有关知识,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
 如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=
如图:已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC= 已知椭圆C:
已知椭圆C: 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2.