题目内容
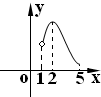
已知f（x）=
在（0，e）上递增，在（e，+∞）上递减（e为自然常数），若不等式x3-2ex2+mx-lnx≥0在（0，+∞）恒成立，则m的取值范围是 ．
| lnx |
| x |
考点：函数恒成立问题
专题：函数的性质及应用
分析：把不等式变形后分离参数m，然后利用函数f（x）=
的单调性及二次函数的最值求得函数-x2+2ex+
的最大值，则答案可求．
| lnx |
| x |
| lnx |
| x |
解答：
解：由x3-2ex2+mx-lnx≥0在（0，+∞）恒成立，
得mx≥-x3+2ex2+lnx在（0，+∞）恒成立，
即m≥-x2+2ex+
在（0，+∞）恒成立，
令函数g（x）=-x2+2ex，t（x）=
，
当x=e时函数g（x）有最大值，同时t（x）取得最大值，
则当x=e时，函数函数-x2+2ex+
有最大值为-e2+2e2+
=e2+
．
∴m≥e．
∴m的取值范围是[e，+∞）．
故答案为：[e，+∞）．
得mx≥-x3+2ex2+lnx在（0，+∞）恒成立，
即m≥-x2+2ex+
| lnx |
| x |
令函数g（x）=-x2+2ex，t（x）=
| lnx |
| x |
当x=e时函数g（x）有最大值，同时t（x）取得最大值，
则当x=e时，函数函数-x2+2ex+
| lnx |
| x |
| lne |
| e |
| 1 |
| e |
∴m≥e．
∴m的取值范围是[e，+∞）．
故答案为：[e，+∞）．
点评：本题考查了函数恒成立问题，考查了分离变量法求参数的取值范围，训练了利用函数的单调性求函数的最值，是中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
设i的虚数单位，复数
为纯虚数，则实数b的值为（ ）
| 1+bi |
| 1+i |
| A、0 | B、1 | C、-1 | D、±1 |
若O为△ABC所在平面内任一点，且满足（
-
）•（
+
-2
）=0，则△ABC一定是（ ）
| OB |
| OC |
| OB |
| OC |
| OA |
| A、正三角形 |
| B、等腰三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |