题目内容
已知函数f(x)=
,则f(-2011)的值为( )
|
| A、2 | ||
| B、8 | ||
C、
| ||
D、
|
考点:抽象函数及其应用,函数的值,分段函数的应用
专题:计算题
分析:将-2011转化到区间[0,2)上,从而可求出所求.
解答:
解:根据题意可得f(-2011)=f(-2001)=…=f(-1)=f(9)
f(9)=f(7)=…=f(1)=
.
故选C.
f(9)=f(7)=…=f(1)=
| 1 |
| 2 |
故选C.
点评:本题主要考查了抽象函数求值,解题的关键是将所求值转化到已知解析式的区间,同时考查了学生分析问题和解决问题的能力,以及运算求解的能力.

练习册系列答案
相关题目
 如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=
如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=| 2x-x2 |
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x>2} |
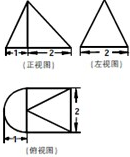
一个几何体的三视图如图,其俯视图是一个等边三角形,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、(4+π)
|
“m=1”是“直线mx+(2m-1)y+1=0和直线3x+my-3=0垂直”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
方程lgx+x=0在下列的哪个区间内有实数解( )
A、[-10,-
| ||
| B、(-∞,0] | ||
| C、[1,10] | ||
D、[
|
函数f(x)=
sin2x+sin2x(x∈R)的图象向左平移
个单位后得到函数y=g(x)的图象,则以下说法错误的是( )
| ||
| 2 |
| π |
| 6 |
A、(
| ||||
| B、函数y=g(x)的最小正周期是π | ||||
C、函数y=g(x)在[-
| ||||
D、直线x=-
|