题目内容
已知m，n是两条不同的直线，α，β，γ是三个不同的平面，下列命题正确的是（ ）
| A、若m∥α，n∥α，则m∥n |
| B、若α⊥β，α⊥γ，则β∥γ |
| C、若m∥α，m∥β，则α∥β |
| D、若m⊥α，m⊥β，则α∥β |
考点：平面与平面之间的位置关系
专题：阅读型,空间位置关系与距离
分析：A．由线面平行的性质，即可判断；B．由面面垂直的性质，结合面面的位置关系即可判断；C．由线面平行的性质和面面平行的判定定理，即可判断；D．由面面平行的判定定理：垂直于同一直线的两平面平行，即可判断．
解答：
解：A．若m∥α，n∥α，则m∥n或m，n异面或m，n相交，故A错；
B．若α⊥β，α⊥γ，则β∥γ或β∩γ=l，故B错；
C．若m∥α，m∥β，则α∥β或α∩β=a，故C错；
D．若m⊥α，m⊥β，则α∥β，故D正确．
故选：D．
B．若α⊥β，α⊥γ，则β∥γ或β∩γ=l，故B错；
C．若m∥α，m∥β，则α∥β或α∩β=a，故C错；
D．若m⊥α，m⊥β，则α∥β，故D正确．
故选：D．
点评：本题考查空间直线与平面的位置关系：平行和垂直，考查线面平行的性质和线面垂直的性质，以及面面平行的判断和性质，和面面垂直的性质，是一道基础题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
现将甲乙丙丁4个不同的小球放入A、B、C三个盒子中，要求每个盒子至少放1个小球，且小球甲不能放在A盒中，则不同的放法有（ ）
| A、12种 | B、24种 |
| C、36种 | D、72种 |
已知sin（α-β）cosα-cos（α-β）sinα=
，且β为第三象限角．则cosβ等于（ ）
| 7 |
| 25 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
若三点P（1，1），A（2，-4），B（x，-14）共线，则（ ）
| A、x=-1 | B、x=3 |
| C、x=4 | D、x=51 |
如图，AB是的直径，PB，PE分别切⊙O于B，C，∠ACE=40°，则∠P=（ ）
| A、60° | B、70° |
| C、80° | D、90° |
已知l是直线，α、β是两个不同平面，下列命题中的真命题是（ ）
| A、若l∥α，l∥β，则α∥β |
| B、若α⊥β，l∥α，则l⊥β |
| C、若l⊥α，l∥β，则α⊥β |
| D、若l∥α，α∥β，则l∥β |
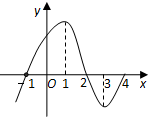如图所示为y=f′（x）的图象，则下列判断正确的是（ ）