题目内容
17．设函数f（x）=$\left\{{\begin{array}{l}{{x^2}+1，x≤1}\\{{2^x}+ax，x＞1}\end{array}}$，若f（f（1））=4a，则实数a=2，函数f（x）的单调增区间为（0，+∞）．分析 求出f（1）=2，再求f（2），解方程可得a；求出分段函数式，求出增区间．
解答 解：函数f（x）=$\left\{{\begin{array}{l}{{x^2}+1，x≤1}\\{{2^x}+ax，x＞1}\end{array}}$，
可得f（1）=2，f（f（1））=f（2）=4+2a=4a，
解得a=2；
f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x≤1}\\{{2}^{x}+2x，x＞1}\end{array}\right.$的增区间为（0，1）∪[1，+∞）
=（0，+∞）．
故答案为：2，（0，+∞）
点评 本题考查分段函数的函数值和单调区间，考查运算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
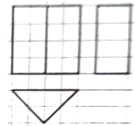如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的表面积为32π．