题目内容
15.求下列函数的定义域:(1)y=$\sqrt{sinx}$;
(2)y=2+$\frac{1}{cosx}$.
分析 (1)由sinx≥0,解得2kπ≤x≤2kπ+π,k∈Z.即可得出函数y=$\sqrt{sinx}$的定义域.
(2)由cosx≠0,解得x≠$kπ+\frac{π}{2}$,k∈Z.即可得出函数y=2+$\frac{1}{cosx}$的定义域.
解答 解:(1)由sinx≥0,解得2kπ≤x≤2kπ+π,k∈Z.
∴函数y=$\sqrt{sinx}$的定义域为{x|2kπ≤x≤2kπ+π,k∈Z}.
(2)由cosx≠0,解得x≠$kπ+\frac{π}{2}$,k∈Z.
∴函数y=2+$\frac{1}{cosx}$的定义域为:{x|x≠$kπ+\frac{π}{2}$,k∈Z}.
点评 本题考查了函数的定义域、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若sinα=2cosα,则$\frac{sinα-cosα}{sinα+cosα}$的值为( )
| A. | 1 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -1 |
6.已知三棱锥O-ABC,OA,OB,OC两两垂直,且OA=OB=$\sqrt{2}$,OC=1,P是△ABC上任意一点,设OP与平面ABC所成角为x,OP=y,则y关于x的函数关系图象为( )
| A. | 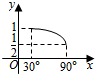 | B. | 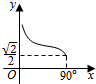 | C. | 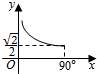 | D. | 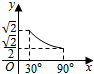 |
4.已知sin($\frac{π}{3}$+a)=$\frac{12}{13}$,a∈($\frac{π}{6}$,$\frac{2π}{3}$),则cosα的值为 ( )
| A. | $\frac{12\sqrt{3}-5}{13}$ | B. | $\frac{12\sqrt{3}-5}{26}$ | C. | $\frac{12\sqrt{3}+5}{13}$ | D. | $\frac{12\sqrt{3}+5}{26}$ |
3.已知i是虚数单位,若复数(a+i)(2-i)是纯虚数,则实数a等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -2 |