题目内容
下列命题:
①?x0∈R,2x0>3x0;
②若函数f(x)=(x-a)(x+2)为偶函数,则实数a的值为-2;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则k=2;
④从1,2,3,4,5,6六个数中任取2个数,则取出的两个数是连续自然数的概率是
,
其中真命题是 (填上所有真命题的序号).
①?x0∈R,2x0>3x0;
②若函数f(x)=(x-a)(x+2)为偶函数,则实数a的值为-2;
③圆x2+y2-2x=0上两点P,Q关于直线kx-y+2=0对称,则k=2;
④从1,2,3,4,5,6六个数中任取2个数,则取出的两个数是连续自然数的概率是
| 1 |
| 3 |
其中真命题是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①取x0=-1满足;
②利用偶函数的定义f(-x)=f(x),可得2-a=0,解得a即可;
③由于此圆上存在两点P,Q关于直线kx-y+2=0对称,可得:此直线经过圆心,即可得出;
④从1,2,3,4,5,6六个数中任取2个数,共有
钟取法,其中取出的两个数是连续自然数的有以下5对:1,2;2,3;3,4;4,5;5,6.利用古典概型的概率计算公式即可得出.
②利用偶函数的定义f(-x)=f(x),可得2-a=0,解得a即可;
③由于此圆上存在两点P,Q关于直线kx-y+2=0对称,可得:此直线经过圆心,即可得出;
④从1,2,3,4,5,6六个数中任取2个数,共有
| C | 2 6 |
解答:
解:①?x0∈R,2x0>3x0,例如x0=-1满足,因此正确;
②若函数f(x)=(x-a)(x+2)为偶函数,则f(-x)=f(x),可得2-a=0,解得a=2,因此不正确;
③由圆x2+y2-2x=0化为(x-1)2+y2=1,可得圆心(1,0),
∵此圆上存在两点P,Q关于直线kx-y+2=0对称,∴此直线经过圆心,
∴k-0+2=0,解得k=-2,因此不正确;
④从1,2,3,4,5,6六个数中任取2个数,共有
钟取法,其中取出的两个数是连续自然数的有以下5对:1,2;2,3;3,4;4,5;5,6.因此取出的两个数是连续自然数的概率P=
=
=
,因此正确.
综上可知:其中真命题是 ①④.
故答案为:①④.
②若函数f(x)=(x-a)(x+2)为偶函数,则f(-x)=f(x),可得2-a=0,解得a=2,因此不正确;
③由圆x2+y2-2x=0化为(x-1)2+y2=1,可得圆心(1,0),
∵此圆上存在两点P,Q关于直线kx-y+2=0对称,∴此直线经过圆心,
∴k-0+2=0,解得k=-2,因此不正确;
④从1,2,3,4,5,6六个数中任取2个数,共有
| C | 2 6 |
| 5 | ||
|
| 5 |
| 15 |
| 1 |
| 3 |
综上可知:其中真命题是 ①④.
故答案为:①④.
点评:本题综合考查了函数的单调性、奇偶性、圆的对称性、古典概型的概率计算公式,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
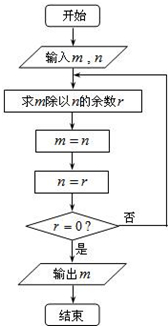 如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )
如图所示的程序框图描述的算法称为欧几里得辗转相除法,若输入m=2010,n=1541,则输出的m的值为( )| A、2010 | B、1541 |
| C、134 | D、67 |
 已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).
已知函数f(x)=x2-2ax+3在区间[-1,1]上有最小值,记作g(a).