题目内容

函数f（x）是二次函数，且在x=1处取得最值，又f(
2
)＜f(π)，则函数f（x）的单调递减区间是
 
．
考点：二次函数的性质
专题：函数的性质及应用
分析：由已知中函数f（x）是二次函数，且在x=1处取得最值，可得x=1是二次函数的对称轴，结合f(
2
)＜f(π)，可分析出函数的单调性
解答： 解：∵函数f（x）是二次函数，且在x=1处取得最值，
∴x=1是二次函数的对称轴，
又1＜
2
＜π，f(
2
)＜f(π)，
∴函数在（1，+∞）上递增，在（-∞，1]上递减．
故答案为：（-∞，1]
点评：本题考查的知识点是二次函数的性质，难度不大，属于基础题．
练习册系列答案
相关题目
求下列函数的值域：
（1）y=5 x2+2x+3；
（2）y=（
1
2
） -x2-2x+3．
下列命题：
①?x0∈R，2x0＞3x0；
②若函数f（x）=（x-a）（x+2）为偶函数，则实数a的值为-2；
③圆x2+y2-2x=0上两点P，Q关于直线kx-y+2=0对称，则k=2；
④从1，2，3，4，5，6六个数中任取2个数，则取出的两个数是连续自然数的概率是
1
3
，
其中真命题是
 
（填上所有真命题的序号）．
已知以下四个命题：
①如果x1，x2是一元二次方程ax2+bx+c=0的两个实根，且x1＜x2，那么不等式ax2+bx+c＜0的解集为{x|x1＜x＜x2}；
②若
x-1
x-2
≤0，则（x-1）（x-2）≤0；
③“若m＞2，则x2-2x+m＞0的解集是实数集R”的逆否命题；
④若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中为真命题的是
 
．（填上你认为正确的序号）．
在平面直角坐标系xOy中，过点P（5，3）作直线l与圆x2+y2=4相交于A，B两点，若OA⊥OB，则直线l的斜率为
 
．
已知集合A={x|x＜2}，B={-1，0，2，3}，则A∩B=
 
．
将两枚各面分别刻有数字1，2，2，3，3，3的骰子掷一次，则掷得的点数之和为5的概率为
 
．
复数z=
2
i2014
1-
2
i
（i是虚数单位）在复平面内的对应点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
阅读如图所示程序框图，运行相应的程序，输出s的值等于（　　）
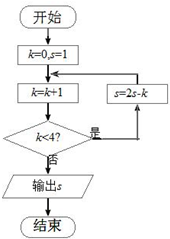
A、-3B、-10C、0D、-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网