题目内容
已知函数f(x)=|x-2|-|x-5|,
(1)求函数f(x)的值域;
(2)解不等式f(x)≥x2-8x+15.
(1)求函数f(x)的值域;
(2)解不等式f(x)≥x2-8x+15.
考点:绝对值不等式的解法,函数的值域,其他不等式的解法
专题:计算题,不等式的解法及应用
分析:(1)通过对自变量x范围的讨论,去掉绝对值符号,利用函数的性质即可求得函数f(x)的值域;
(2)通过对自变量x范围的讨论,去掉绝对值符号,再解相应的二次不等式即可.
(2)通过对自变量x范围的讨论,去掉绝对值符号,再解相应的二次不等式即可.
解答:
解:(1)∵f(x)=|x-2|-|x-5|,
∴当x≤2时,f(x)=2-x-(5-x)=-3;
当2<x<5时,f(x)=x-2-(5-x)=2x-7∈(-3,3);
当x≥5时,f(x)=x-2-(x-5)=3;
综上所述,函数f(x)的值域为[-3,3];
(2)∵|x-2|-|x-5|≥x2-8x+15,
∴当x≤2时,x2-8x+15≤-3,
解得x∈∅;
当2<x<5时,有x2-8x+15≤2x-7,
解得5-
≤x<5;
当x≥5时,有x2-8x+15≤3,
即得5≤x≤6,
综上所述,原不等式的解集为{x|5-
≤x≤6}.
∴当x≤2时,f(x)=2-x-(5-x)=-3;
当2<x<5时,f(x)=x-2-(5-x)=2x-7∈(-3,3);
当x≥5时,f(x)=x-2-(x-5)=3;
综上所述,函数f(x)的值域为[-3,3];
(2)∵|x-2|-|x-5|≥x2-8x+15,
∴当x≤2时,x2-8x+15≤-3,
解得x∈∅;
当2<x<5时,有x2-8x+15≤2x-7,
解得5-
| 3 |
当x≥5时,有x2-8x+15≤3,
即得5≤x≤6,
综上所述,原不等式的解集为{x|5-
| 3 |
点评:本题考查绝对值不等式的解法,突出考查转化思想与分类讨论思想的综合应用,考查解一元二次不等式的运算能力,属于中档题.

练习册系列答案
相关题目
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=2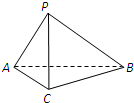 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,