题目内容
圆心在直线y=x上,圆与直线E:x+2y-1=0相切,圆在y轴上截得的弦长为2,求圆的标准方程.
考点:圆的标准方程
专题:直线与圆
分析:本题先用待定系数法设出圆的标准方程,再利用圆心在直线上,得到一个关系式,用圆与直线相切得到一个关系式,再通过弦长和勾股定理得到一个关系式,解关系式组求出参数,得到圆的方程.
解答:
解:由于圆心在直线y=x上所以可以设圆心的坐标为(a,a)
设圆的半径为r,
∵圆与直线E相切,
∴圆心(a,a)到直线的距离d=
=
=r(1)
又因为圆y轴截得的弦长为2,半弦长为1,
所以a2+1=r2将其带入(1)式得
=a2+1,
解得a=2或a=-
.
∴圆的标准方程为(x-2)2+(y-2)2=5或(x+
)2+(y+
)2=
设圆的半径为r,
∵圆与直线E相切,
∴圆心(a,a)到直线的距离d=
| |a+2a-1| | ||
|
| |3a-1| | ||
|
又因为圆y轴截得的弦长为2,半弦长为1,
所以a2+1=r2将其带入(1)式得
| (3a-1)2 |
| 5 |
解得a=2或a=-
| 1 |
| 2 |
∴圆的标准方程为(x-2)2+(y-2)2=5或(x+
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查了圆的方程知识和函数方程思想,本题思维难度不大,但有一定的计算量,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
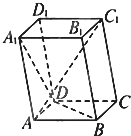 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.