题目内容
若函数f(x)满足:存在T∈R,T≠0,对定义域内的任意x,f(x+T)=f(x)+f(T)恒成立,则称f(x)
为T函数.现给出下列函数:①y=
; ②y=ex;③y=lnx;④y=sinx.其中为T函数的序号是 .(把你认为正确的序号都填上)
为T函数.现给出下列函数:①y=
| 1 |
| x |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:通过赋值法,求出f(0)的函数值,逐一判断4个函数推出结果.
解答:
解:函数f(x)满足:存在T∈R,T≠0,对定义域内的任意x,f(x+T)=f(x)+f(T)恒成立,
令x=0,可得:f(0+T)=f(0)+f(T),∴f(0)=0;f(T)是常数.
若f(T)>0,则函数是增函数;
若f(T)=0,则函数是周期函数;
若f(T)<0,则函数是减函数;
①y=
;x=0函数没有意义,在定义域内,不是增函数、减函数、周期函数,∴①不正确;
②y=ex;f(0)=1,②不正确;
③y=lnx;x=0函数没有意义,函数是增函数,但是从变化趋势看不是线性关系,∴③不正确;
④y=sinx.f(0)=0,并且函数是周期函数,符合题意;④正确.
综上所述,属于为T函数的序号是④.
故答案为:④.
令x=0,可得:f(0+T)=f(0)+f(T),∴f(0)=0;f(T)是常数.
若f(T)>0,则函数是增函数;
若f(T)=0,则函数是周期函数;
若f(T)<0,则函数是减函数;
①y=
| 1 |
| x |
②y=ex;f(0)=1,②不正确;
③y=lnx;x=0函数没有意义,函数是增函数,但是从变化趋势看不是线性关系,∴③不正确;
④y=sinx.f(0)=0,并且函数是周期函数,符合题意;④正确.
综上所述,属于为T函数的序号是④.
故答案为:④.
点评:本题考查抽象函数的应用,新定义的理解与掌握是解题的关键,同时注意特值法的应用.

练习册系列答案
相关题目
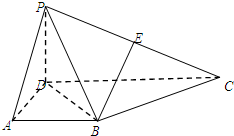 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.