题目内容
求以椭圆
+
=1,的焦点为顶点,以椭圆的顶点为焦点的双曲线方程,并求它的离心率、渐近线方程.
| x2 |
| 49 |
| y2 |
| 24 |
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定椭圆的焦点、顶点坐标,可得双曲线的顶点、焦点坐标,即可求出双曲线的离心率、渐近线方程.
解答:
解:椭圆
+
=1的焦点坐标为(±5,0),两个顶点为(±7,0),
∴双曲线的顶点为(±5,0),焦点坐标为(±7,0),
∴双曲线的方程为
-
=1,
∴a=5,b=2
,c=7,
∴e=
=
,渐近线方程为y=±
x.
| x2 |
| 49 |
| y2 |
| 24 |
∴双曲线的顶点为(±5,0),焦点坐标为(±7,0),
∴双曲线的方程为
| x2 |
| 25 |
| y2 |
| 24 |
∴a=5,b=2
| 6 |
∴e=
| c |
| a |
| 7 |
| 5 |
2
| ||
| 5 |
点评:本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
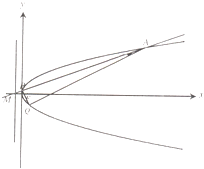 在平面直角坐标系xOy中,已知抛物线C:y2=2px(p>0),在此抛物线上一点M(2,m)到焦点的距离是3.
在平面直角坐标系xOy中,已知抛物线C:y2=2px(p>0),在此抛物线上一点M(2,m)到焦点的距离是3.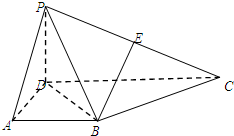 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.