设△ABC的内角A.B.C对边分别为a.b.c.且3b2+3c2-3a2=42bc．(1)求sinA的值,(2)求2sin(B+C)1-cos2A的值．题目和参考答案——青夏教育精英家教网—

题目内容

设△ABC的内角A，B，C对边分别为a，b，c，且3b²+3c²-3a²=4

bc．
（1）求sinA的值；
（2）求

2sin(B+C)

1-cos2A

的值．

考点：余弦定理,两角和与差的正弦函数

专题：解三角形

分析：（1）由余弦定理a²=b²+c²-2bccosA与题中等式比较，可得cosA，结合A是三角形的内角，利用同角三角函数的基本关系式可得A的正弦函数值．
（2）利用二倍角的余弦函数以及诱导公式化简求出所求表达式的分子与分母的值即可．

解答： 解：（1）∵由余弦定理，得a²=b²+c²-2bccosA，
又3b²+3c²-3a²=4

bc，
∴cosA=

，
又∵A是三角形的内角，∴sinA=

1-cos2A

．
（2）∵cosA=

，∴cos2A=2×（

）²-1=

．
sin（B+C）=sinA，
∴

2sin(B+C)

1-cos2A

2×

．

点评：本题考查余弦定理以及同角三角函数的基本关系式的应用，考查计算能力．

练习册系列答案

相关题目

（a-2i）i=b-i，其中a、b∈R，i是虚数单位，则a²+b²=（　　）

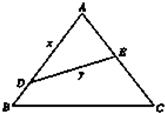如图，公园要把一块边长为2a的等边三角形ABC的边角地修成草坪，DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
（1）设AD=x（x≥a），DE=y，试用x表示函数y；
（2）如果DE是灌溉水管，希望它最短，D、E的位置应该在哪里？

设函数f（x）是定义在区间（-∞，+∞）上的偶函数，且满足f（1-x）=f（1+x）（x∈R）．
（1）求函数f（x）的周期；
（2）已知当x∈（-1，1]时，f（x）=1-

1-x2

，求使方程f（x）=ax在x∈（-1，1]上有两个不相等实根a的取值集合M；
（3）记I_k=（2k-1，2k+1]（k∈N，k≥1），M_k表示使方程f（x）=ax在x∈I_k上有两个不相等实根的a的取值集合，求集合M_k．

已知函数f（x）=

1-sin2x

cosx

（Ⅰ）若f（x）＞0，求x的取值范围；
（Ⅱ）设α是第四象限的角，且tanα=-

，求f（α）的值．

已知函数f（x）=x³+2x²-4x+5．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）求函数y=f（x）在[-4，1]上的最大值和最小值．

已知集合A={1，b}（b＞1），函数f（x）=

（x-1）²+1，当x∈A时，f（x）∈A，求b的取值范围．

有甲、乙两种商品，经销这两种商品所获的利润依次为p（万元）和q（万元），它们与投入的资金x（万元）的关系，据经验估计为：p=-x²+4x，q=2x今有3万元资金投入经销甲、乙两种商品，为了获得最大利润，应对甲、乙两种商品分别投入多少资金？总共获得的最大利润是多少万元？

试题分类