题目内容
20．
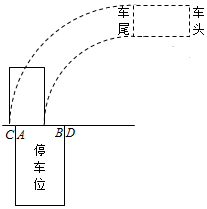某市小型机动车驾照“科二”考试共有5项考察项目，分别记作①，②，③，④，⑤（Ⅰ）某教练将所带10名学员“科二”模拟考试成绩进行统计（如表所示），并打算从恰有2项成绩不合格的学员中任意抽出2人进行补测（只侧不合格项目），求补测项目种类不超过3项的概率．
| 项目/学号编号 | ① | ② | ③ | ④ | ⑤ |
| （1） | T | T | T | ||
| （2） | T | T | T | ||
| （3） | T | T | T | T | |
| （4） | T | T | T | ||
| （5） | T | T | T | T | |
| （6） | T | T | T | ||
| （7） | T | T | T | T | |
| （8） | T | T | T | T | T |
| （9） | T | T | T | ||
| （10） | T | T | T | T | T |
| 注：“T”表示合格，空白表示不合格 | |||||
分析 （I）使用列举法求出古典概型的概率；
（II）使用几何法求出几何概型的概率．
解答 解：（I）由题意得共有5名学员（1），（2），（4），（6），（9）恰有2两项成绩不合格，从中任意抽取2人进行补测，共有10种情况：
| 学员编号 | 补测项目 | 项数 |
| （1）（2） | ②③⑤ | 3 |
| （1）（4） | ②③④⑤ | 4 |
| （1）（6） | ③④⑤ | 3 |
| （1）（9） | ①③⑤ | 3 |
| （2）（4） | ②④⑤ | 3 |
| （2）（6） | ②③④⑤ | 4 |
| （2）（9） | ①②⑤ | 3 |
| （4）（6） | ②③④ | 3 |
| （4）（9） | ①②④⑤ | 4 |
| （6）（9） | ①③④⑤ | 4 |
∴补测项目不超过3项的概率为P=$\frac{6}{10}=\frac{3}{5}$．
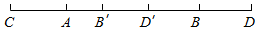
（II）在线段CD上取两点B′，D′，使得BB′=DD′=1.8m，
记汽车尾部左端点为M，则当M位于线段AB′上时，学员可按教练要求完成任务．
∴学员甲能按要求完成任务的概率P=$\frac{AB′}{CD′}$=$\frac{2.4-1.8}{2.4+2×0.3-1.8}$=$\frac{1}{2}$．
点评 本题考查了古典概型和几何概型的概率计算，属于基础题．
练习册系列答案
相关题目
10．已知函数f（x）=ex-2ax，函数g（x）=-x3-ax2．若不存在x1，x2∈R，使得f′（x1）=g′（x2），则实数a的取值范围为（ ）
| A． | （-2，3） | B． | （-6，0） | C． | [-2，3] | D． | [-6，0] |
11．已知i为虚数单位，则i2016=（ ）
| A． | 1 | B． | -1 | C． | i | D． | -i |
15．若命题$p：?x∈（0，+∞），{log_2}（x+\frac{1}{x}）≥1$，命题$q：?{x_0}∈R，x_0^2-{x_0}+1≤0$，则下列命题为真命题的是（ ）
| A． | p∨q | B． | p∧q | C． | （￢p）∨q | D． | （￢p）∧（￢q） |
12．若函数y=2x图象上存在点（x，y）满足约束条件$\left\{\begin{array}{l}{x+y-3≤0}\\{x-2y-3≤0}\\{x≥2m}\end{array}\right.$，则实数m的最大值为（ ）
| A． | 1 | B． | $\frac{3}{2}$ | C． | 2 | D． | $\frac{1}{2}$ |
9．已知△ABC的顶点分别为A（2，1），B（3，2），C（-3，-1），BC边上的高为AD，则点D的坐标为（ ）
| A． | （-$\frac{9}{5}$，$\frac{7}{5}$） | B． | （$\frac{9}{2}$，-$\frac{7}{5}$） | C． | （$\frac{9}{5}$，$\frac{7}{5}$） | D． | （-$\frac{9}{2}$，-$\frac{7}{5}$） |